Contents
- 1 Filosofia Geral da Aplicação do Raciocínio Sub-simbólico a Padrões
- 2 Simuladores de Redes Neurais
- 3 Classificadores: Usando Aprendizado Supervisionado para Reconhecer Padrões
- 4 Desenvolvimento de Aplicações Usando Aprendizado Supervisionado
- 4.1 Aprendizado de Conjuntos Intrincados
- 4.2 Aprendizado de Conjuntos Intrincados Apresentando Erro
- 4.3 Uma Aplicação de Reconhecimento de Padrões Simples: Reconhecer CEPs em Cartas
- 4.4 Outra Aplicação: Determinação Automatizada do Grau de Malignidade (Gradação) de Tumores
- 4.5 Breve Comparação entre Redes-BP, redes-RBF e métodos simbólicos utilizando Nearest Neighbour
- 5 Agrupadores: Usando Aprendizado Não Supervisionado para Organizar Padrões
- 5.1 O Modelo de Kohonen e Quantização de Vetores
- 5.2 Os Mapas Auto-Organizantes de Kohonen
- 5.2.1 Resumo
- 5.2.2 Hipóteses sobre a representação interna de Elementos da lingüística e estruturas
- 5.2.3 Categorias e suas relações para representações neurais e lingüísticas
- 5.2.4 Exemplos de modelos de redes neurais para representações internas
- 5.2.5 Mapas de auto organização (características topológicas)
- 5.2.6 As funções de processamento da informação estão localizadas no cérebro? Justificação do modelo.
- 5.2.7 Mapas topográficos em Áreas sensoriais
- 5.2.8 Representação de dados topologicamente relacionados em um mapa auto organizável
- 5.3 Mapas de auto organização semântica
- 5.4 Discussão: Kohonen é um Modelo Biologicamente Plausível ?
- 5.5 Variação da Função de Vizinhança durante o Treinamento
- 6 O que aprende uma Rede de Kohonen ?
- 7 Explorando Dados Agrupados em Redes
- 7.1 O que aprende uma Rede de Kohonen ?
- 7.2 Qualidades Matemáticas do Modelo de Kohonen
- 7.3 Técnicas de Exploração de Dados Agrupados em Redes
- 7.4 Qual é o objetivo de KoDiag ?
- 7.5 Como funciona KoDiag ?
- 7.6 Utilizando Redes de Kohonen para a coordenação visumotora de um braço de Robô
- 7.7 Referências
- 7.8 Exercício
- 8 Páginas Correlatas neste Site
Filosofia Geral da Aplicação do Raciocínio Sub-simbólico a Padrões
Chamamos de Raciocínio Sub-simbólico ao processamento de informação em um nível onde os padrões representam conjuntos de dados mas onde não podemos associar um significado imediato a cada dado processado. Isto significa que trabalhamos com dados, que em seu conjunto podem ser chamados de informação e assumir um significado, mas onde não sabemos ou não podemos determinar o significado de cada parte do conjunto de informação em separado. O mesmo vale para as representações internas, intermediárias desses dados: usamos sistemas que representam essa informação, mas eles são sistemas black box – caixa preta – produzindo classificações dos padrões e resultados numéricos, sem no entanto fazer isto de forma explícita. As redes neurais são o melhor exemplo de um sistema sub-simbólico: mesmo que cada parte de um padrão apresentado a uma rede tenha um significado explícito, associável a um símbolo de nosso modelo do mundo real, a representação interna dos dados no processador (a rede) não é explícita e não possui significado. Um método subsimbólico tipicamente é incapaz de explicar porque chegou a uma determinada conclusão, uma vez que um mapeamento explícito de causa-e-efeito não existe.
Fica mais fácil ilustrar este conceito através de um exemplo. Imagine um sistema militar para classificar tipos de navios (“inimigos”) a partir do padrão de ruído emitido por estes, da forma como é captado por um submarino (“nosso”). Hipotetize que nós sabemos que um determinado padrão de ruídos corresponde a um porta-aviões de determinada classe de uma determinada nacionalidade. Este padrão inclue um conjunto de freqüências e as variações de amplitude dessas freqüências, além de algumas outras informações. Nós podemos associar um conjunto de símbolos a esse padrão: “Porta-Aviões modelo Banheirão de Corto Maltese“, mas classificamos o padrão como um todo. Nós não sabemos dizer que papel tem uma freqüência X qualquer do ruído neste padrão ou que parte mecânica do navio em questão ela representa. Talvez não saibamos nem mesmo, se vamos continuar conseguindo classificar o padrão, caso retiremos os valores correspondentes a esta freqüência do padrão.
Este é um exemplo típico. Mesmo em situações onde os dados possuem um significado conhecido, como no caso de dados de um paciente cardíaco potencial, onde eu sei o significado da freqüência cardíaca, mas onde eu não sei o relacionamento entre a freqüência cardíaca e a chance deste paciente ter um infarte numa determinada situação futura. É esse relacionamento, que eu não posso mapear de forma explícita que eu quero que um sistema subsimbólico mapeie implicitamente para mim. E os sistemas subsimbólicos fazem isto, mas o fazem de forma fechada, sem gerar mapas, tabelas estatísticas ou conjuntos de regras de como criam este mapeamento.
As Redes Neurais Artificiais são o mais difundido e popular conjunto de métodos subsimbólicos, sendo em geral caixas-pretas por excelência. Existem outros métodos que não vamos abordar aqui. O fato das redes neurais serem caixas pretas muitas vezes é citado como uma de suas desvantagens. Neste capítulo nós vamos ver que isto é relativo. Este capítulo pressupõe que você já viu Teoria das Redes Neurais na cadeira de Inteligência Artificial e que você tem o conhecimento teórico básco sobre os métodos: aqui nós vamo ver aplicações de redes neurais e técnicas de integração das mesmas em sistemas mais complexos.
Simuladores de Redes Neurais
SNNS – Stutgarter Neural Network Simulator
O SNNS é um dos melhores simuladores de Redes Neurais existentes. Porisso nós vamos vê-lo aqui. O objetivo de alocarmos um capítulo a ele é o de prover ao aluno com uma ferramenta poderosa para a execução dos exercícios propostos, livrando-o da necessidade de ter de programar ele mesmo as redes.
O SNNS possui outra vantagem: após treinada um rede, você pode gerar com o SNNS um arquivo em linguagem “C” contendo a rede treinada. Este arquivo compilado pode ser utilizado como prorama standalone ou então como biblioteca (.dll ou .so) linkada ao programa aplicativo que você for usar. Isto é uma vantagem para as aplicações em Smalltalk que você vai desenvolver, pois permite que você utilize o pacote “DLL & C connect” para usar estas redes em Smalltalk.
- Versão do SNNS em Java para Windows
- Java Runtime Environment completo que você precisa para o software acima
- Versão compilada do SNNS 4.2 para Linux (se você possue RedHat ou Conectiva instalado pode ter problemas para rodar pois a versão do Athena suprida com RedHat e seus clones é meio estranha. Teste estas opções: a) Mude a profundidade de seu vídeo para 8 bits ou b) Não carregue os arquivos de configuração dos exemplos, apenas as redes e os arquivos de treinamento.
TensorFlow Simplificado
Você pode também fazer alguns testes usando o simulador de TensorFlow:
Classificadores: Usando Aprendizado Supervisionado para Reconhecer Padrões
Há dois modelos de redes neurais utilizados na prática como classificadores passíveis de serem gerados através de aprendizado supervisionado. Ambos os modelos baseiam-se nos Perceptrons feed-forward, variando o número de camadas e a função de ativação e, por conseguinte, a regra de aprendizado: a) As Redes Backpropagation e b) as Redes de Base Radial.
Por serem as mais utilizadas e, do ponto de vista prático, mas mais importantes, vamos nos ocupar aqui das Redes Backpropagation, também chamadas redes-BP. As redes de Base Radial, conhecidas também por redes-RBF podem ser usadas, em teoria, para representar os mesmos tipos de problemas que uma rede Backpropagation equivalente. Alguns autores argumentam que são mais eficientes durante o treinamento. Por outro lado, a compreensão de seu algoritmo de aprendizado envolve uma matemática bastante mais complexa. Como são utilizadas para resolver o mesmo tipo de problemas que os onde Backpropagation encontra aplicação, sem vantagens consideráveis na qualidade do resultado final, vamos ignorá-las aqui. No final desta seção há uma comparação entre redes-RBF e redes-BP, extraída de [Haykin] e um comentário nosso sobre redes-RBF e sua relação com Nearest Neighbour e métodos que utilizam NN, como IBL*.
Como esta disciplina pressupõe que você já viu o assunto Redes Neurais, vamos aqui apenas recordar alguns conceitos matemáticos importantes para que você entenda a nossa discussão mais adiante de como se deve aplicar corretamente Backpropagation.
Princípios Matemáticos de Redes-BP
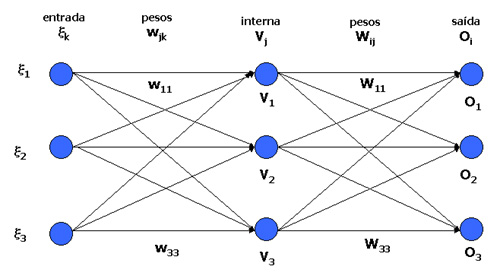
Existem várias convenções amtemáticas para a nomenclatura dos elementos de uma rede neural. Durante todo o capítulo de Redes Neurais vamos utilizar a simbologia matemática descrita em [Hertz et.ali.].
Um conjunto de treinamento é um conjunto p de padrões, todos de mesmo tamanho, cada qual dividido em duas partes: vetor de entrada  e vetor de saída
e vetor de saída  . O vetor de saída representa a atividades esperada nos neurônios de saída quando é apresentado o vetor de entrada nos neurônios de entrada da rede.
. O vetor de saída representa a atividades esperada nos neurônios de saída quando é apresentado o vetor de entrada nos neurônios de entrada da rede.
O conjunto de treinamento pode ser visto como:

Princípios Básicos das Redes Backpropagation
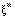 gerada por este padrão na camada de neurônios de entrada, camada a camada, até gerarmos uma ativação nos neurônios da camada de saída.
gerada por este padrão na camada de neurônios de entrada, camada a camada, até gerarmos uma ativação nos neurônios da camada de saída.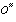 gerada para o vetor de entrada
gerada para o vetor de entrada 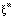 do padrão m pela rede seja o mais próximo possível do vetor de saída
do padrão m pela rede seja o mais próximo possível do vetor de saída 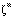 deste padrão, de forma que no futuro, quando apresentarmos um outro vetor similar a
deste padrão, de forma que no futuro, quando apresentarmos um outro vetor similar a 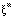 , a rede produza uma resposta o mais próxima possível de
, a rede produza uma resposta o mais próxima possível de 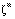 .
. Para realizarmos esta modificação dos pesos, representamos o erro de saída da rede como uma função do conjunto dos pesos, E(w), e utilizamos a técnica denominada descida em gradiente (gradient descent ou Gradientenabstieg) para realizar alterações iterativas dos pesos de forma a reduzir o erro. Para isto, representamos inicialmente E(w) como uma função-custo baseada na soma dos quadrados dos erros:
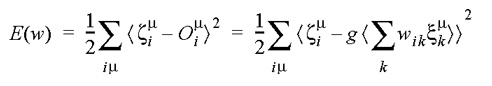
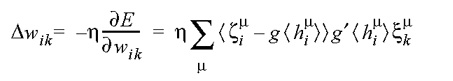
- introduzimos uma taxa de aprendizado h, tipicamente de valor < 0,2
- apresentamos os padrões de treinamento em ordem aleatória, garantindo que tenhamos apresentado todos antes de reapresentarmos algum.
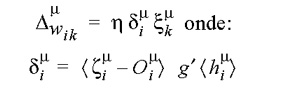 No treinamento de redes neurais, ao invés de falarmos de iterações, chamamos a cada ciclo de apresentação de todos os padrões de época. Antes de iniciar uma nova época, reorganizamos os padrões em uma nova ordem aleatória. A cada época todos os padrões são apreseentados.
No treinamento de redes neurais, ao invés de falarmos de iterações, chamamos a cada ciclo de apresentação de todos os padrões de época. Antes de iniciar uma nova época, reorganizamos os padrões em uma nova ordem aleatória. A cada época todos os padrões são apreseentados.Aprendizado das Redes-BP
O fato que fez com que a pesquisa em redes neurais ficasse quase 20 anos (1968 – 1984) parada no cenário internacional foi o seguinte conjunto de fatos:
- para que uma rede neural feedforward possa representar uma função qualquer (universalidade representacional) ela necessita de pelo menos uma camada intermediária, além da camada de entrada e da de saída e a função de ativação de pelo menos parte dos neurônios deve ter caráter não-linear.
- para que a rede possa aprender, é necesário que possamos calcular a derivada do erro em relação aos pesos em cada camada, de tràs para frente, de forma a minimizar a função custo definida na camada de saída. Para isto ser possível, a função de ativação deve ser derivável.
- introduzir uma não linearidade sem no entanto alterar de forma radical a resposta da rede (ela se comporta de forma similar a uma rede linear para casos “normais”) e
- possibilitar o cálculo da derivada parcial do erro em relação aos pesos (o que nós queríamos desde o começo) de uma forma elegante e generalizável para todas as camadas.
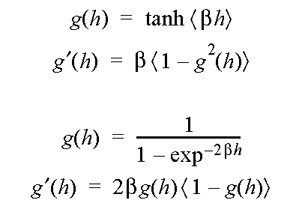

Aprendizado para Redes de Várias Camadas
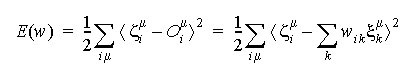




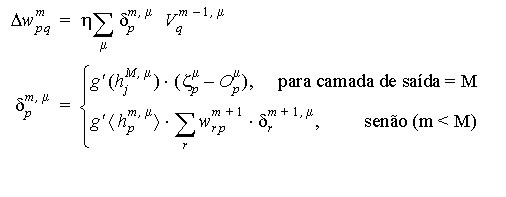
Algoritmo Backpropagation
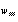
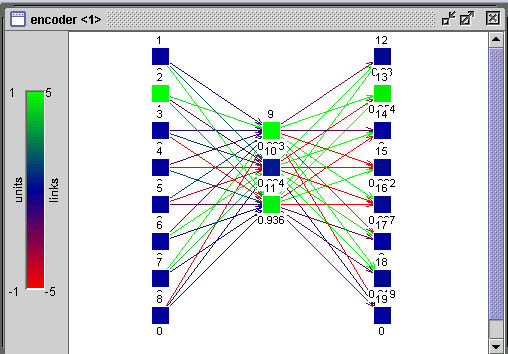
- uma função de ativação não-linear contínua e diferenciável no domínio dos valores a serem treinados na rede
- uma taxa de aprendizado h
- um conjunto de treinamento contendo xm entradas e zm saídas.



O que Aprende uma Rede-BP ?
Como citamos em outras partes deste texto, uma rede backpropagation, ao contrário de redes-RBF ou classificadores baseados em Nearest Neighbour, como IBL, aprende uma função capaz de mapear a entrada à saída, caso esta exista. Se o conjunto de treinamento for inconsistente a rede não aprenderá nada ou aprenderá cada exemplo individual do conjunto de treinamento, caso a criemos grande o suficiente.
Em princípio, o mapeamento entrada-saída em uma rede-BP está distribuído sobre o total dos pesos e conexões da rede, sendo bastante difícil associarmos um determinado neurônio e suas conexões a uma determinada classe.
Do ponto de vista matemático, existem várias interpretações do significado dos pesos aprendidos por uma rede neural. Uma discussão detalhada deste assunto foge do escopo de uma disciplina de graduação e nós remetemos à literatura, principalmente [Hertz et.ali.].
Existem, porém, algumas situações interessantes, onde o aprendizado da rede neural pode ser visualizado e podemos realmente associar um ou um conjunto de neurônios a uma determinada classe. Isto tende a acontecer quando o conjunto de treinamento contém classes realmente muito bem comportadas.
O exemplo clássico para este comportamento é o encoder (codificador). Este exemplo está incluído na coleção de exemplo sprontos do SNNS e sugerimos ao leitor que faça alguns experimentos com ele. O encoder é um exemplo onde podemos fazer os padrões de ativação dos neurônios da camada interna representarem uma compressão dos dados de treinamento e ainda utilizar esta compressão de dados como um código representando os mesmos.
O encoder toma um valor de entrada de 0 a 7 e aprende a asociá-lo a mesma saída, possuíndo 8 neurônios de entrada, um para cada valor e 8 neurônios de saída, com a mesma representação. Na camada intermediária possui apenas 3 neurônios. O objetivo é que, ao aprender a associação entrada-saída, ele codifique os dados. A figura abaixo mostra o encoder recebendo o número 1 como padrão de entrada (01000000) e representando internamente este número como 101.
O conjunto de treinamento do encoder não é só linearmente separável, mas é também linearmente independente e, portanto, um conjunto extremamente fácil de aprender, que não necessitaria de uma camada interna, podendo ser representado por um perceptron simples. Mesmo assim é interessante de se observar o fenômeno da representação interna. Este fenômeno porém não ocorre sempre dessa forma, com a rede “inventando” seu próprio código binário. Às vezes os pesos se distribuem de uma forma tal na rede que não é possível uma interpretação visual da “representação interna”.
Exercício: Observando o Encoder
Vamos ver com que freqüência o encoder realmente aprende uma representação interna que para nós, humanos, faz “sentido”. Carregue o exemplo do encoder no SNNS. Reinicialize a rede e treine-o. Bastam 100 épocas pois o conjunto é aprendido extremamente rápido. Feito isto, vá para o modo “updating” e repasse todo o conjunto de treinamento pela rede. Foi possível criar-se um arepresnetação interna similar a algum código binário conhecido ? Repita este processo várias vezes, reincializando, treinando e testando a rede para ver como ela se comporta.
Aspectos Práticos de Métodos de Descida em Gradiente
Como citamos brevemente antes, o processo de redução do erro E(w) pertence a uma categoria de métodos matemáticos denominado Métodos de Descida em Gradiente (Gradient Descent Methods). Nocaso específico das redes-BP, que nos interessa, podemos imaginar a idéia de que o erro é uma (hiper) superfície em um espaço definido pelos pesos [w] da rede neural. O estado atual da rede (conjunto de valores específico dos pesos das conexões entre os neurônios) é um ponto sobre esta superfície. O nosso objetivo é mover este ponto através da alteração dos valores do spesos de forma a encontrar uma posição onde o erro seja o menor possível. O movimento é realizado sempre no sentido de reduzir-se o erro, ou seja sempre descendo a superfície de erro de forma que o próximo ponto seja uma posição mais funda nesta superfície, até encontrar uma posição de onde não sejja possível descer-se mais. Se imaginarmos uma situação 3D, onde há apenas dois pesos definindo os espaços x e Y e a coordenada z sendo definida pelo erro, podemos imaginar o processo como o mostra a figura abaixo.
O material abaixo é um resumo do tutorial de redes neurais disponibilizado pela Neuro-Fuzzy AG (Grupo de Trabalho Neuro-Fuzzy) do Departamento de Matemática da Universidade de Muenster, Alemanha.
| Mínimo Local: Partindo-se da configuração de pesos inicial w1, o método de descida em gradiente não encontrará a solução (mínimo global). | 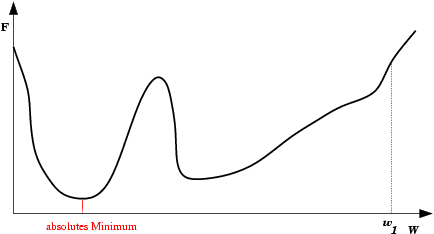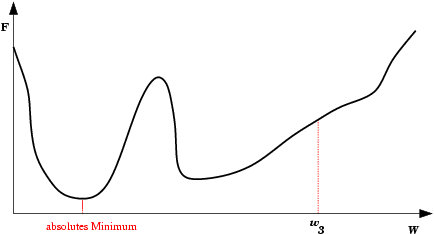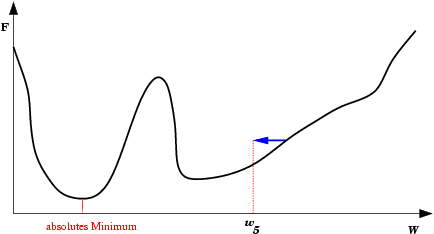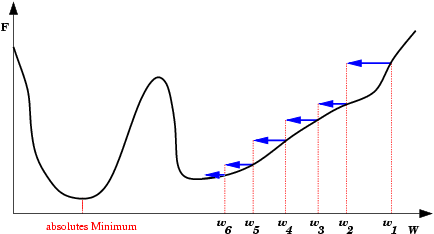 |
| Platô encontrado em E(w) durante treinamento da rede neural. Durante um longo período não haverá mudanças significativas em E(w). Após um tempo, porém, o mínimo absoluto (global) é encontrado. | 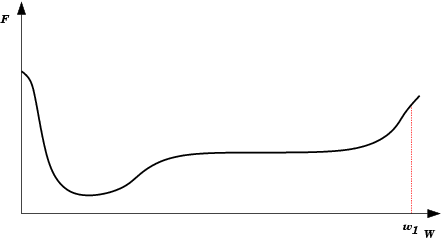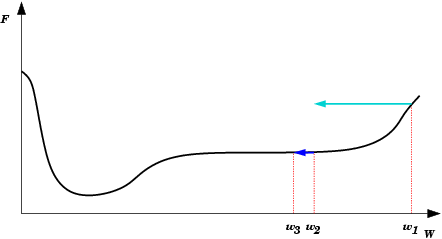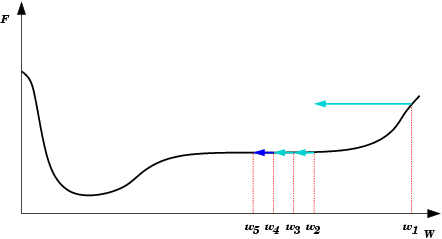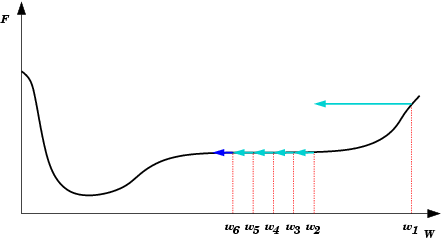 |
| Oscilações ocorrem quando o processo de descida de gradiente cai em uma ravina de onde não sai mais. Também é uma espécie de mínimo local. O passo de modificação dos pesos (taxa de aprendizado) é grande demais para que a rede caia na ravina, mas pequena demais para sair do mínimo. Ao conrário do mínimo local comum, aqui a rede não encontra um estado estável. | 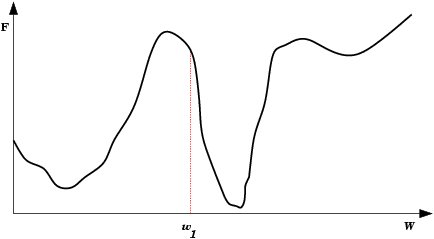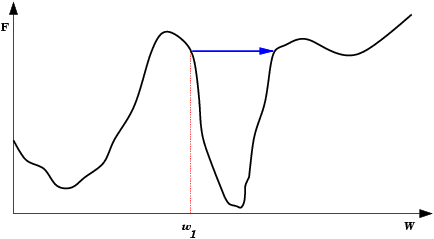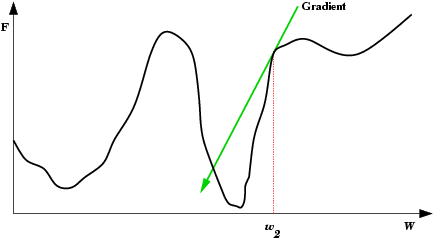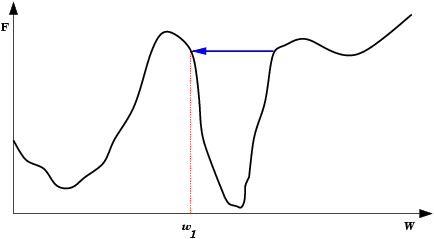 |
| A Oscilação Indireta é uma situação de oscilação mais complexa, onde a rede também fica “presa” em um mínimo local e não encontra um estado estável. Neste caso porém, existem estados intermediários entre os estados extremos da oscilação, onde o erro por momentos se permite reduzir. | 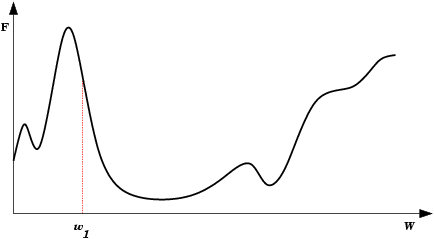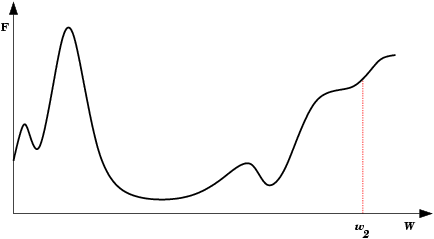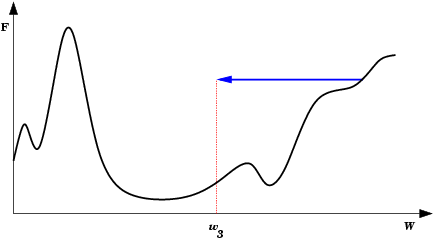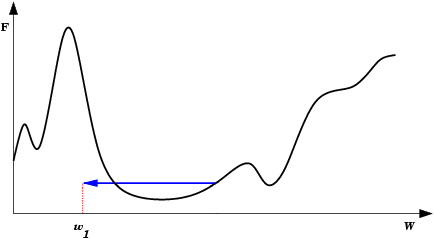 |
| Saída do mínimo ótimo para um subótimo. Se a mudança dos pesos se inicia numa área de gradiente muito grande, os primeiros ajustes podem ser excessivamente grandes e levar a rede a passar do vale onde está o mínimo global, para uma região com um mínimo local. | 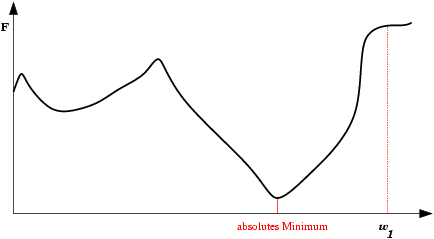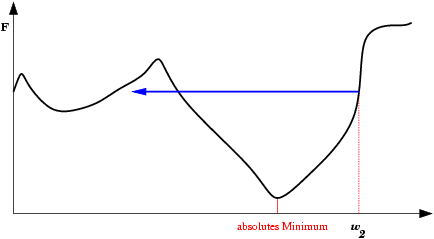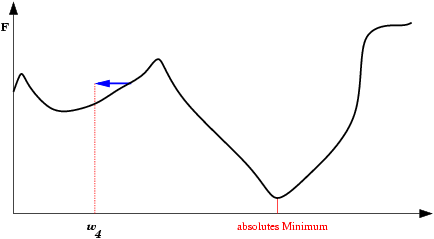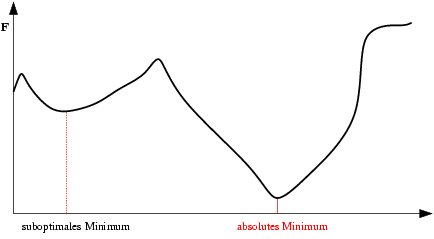 |
Existem várias técnicas para “turbinar”a descida em gradiente de forma e evitar alguns dos problemas descritos acima. Estas técnicas são implementadas em parte no SNNS. Na aula vamos discutir suas vantagens e limitações.
Desenvolvimento de Aplicações Usando Aprendizado Supervisionado
Importante: O texto abaixo está estruturado de forma a complementar o assunto visto em aula de laboratório. O material não pretende ser auto-explicativo nem didaticamente autosuficiente: esta seção supõe que a aula a que ela se refere foi assistida pelo aluno e serve apenas de referência.
Aprendizado de Conjuntos Intrincados
O conjunto de dados distribuído sob a forma de duas espirais duplas, como já foi dito anteriormente, é um conjunto clássico de teste para redes neurais. Vamos tentar avaliar a competência de todos so métodos que veremos nesta disciplina utilizando este conjunto de dados. Até agora você viu como técnicas simples como kNN e como métodos simbólicos que utilizam Nearest Neighbour, como IBL se comportam frente a este conjunto de dados. Nesta seção veremos como se comporta uma rede-BP frente ao mesmo conjunto de dados. O objetivo desta comparação é fornecer-lhe dados para avaliar a performance e adequação desta técnica.
Para isto utilizaremos uma rede neural como mostra a figura abaixo. Esta rede está organizada em 3 camadas, possuindo apenas uma camada interna. A organização desta camada interna como uma matriz é somente um subterfúgio gráfico para fazer a rede caber na janela do simulador, a posição de um neurônio nesta matriz, ao contrário do que ocorrerá mais adiante em redes de Kohonen, não possui nenhum significado.
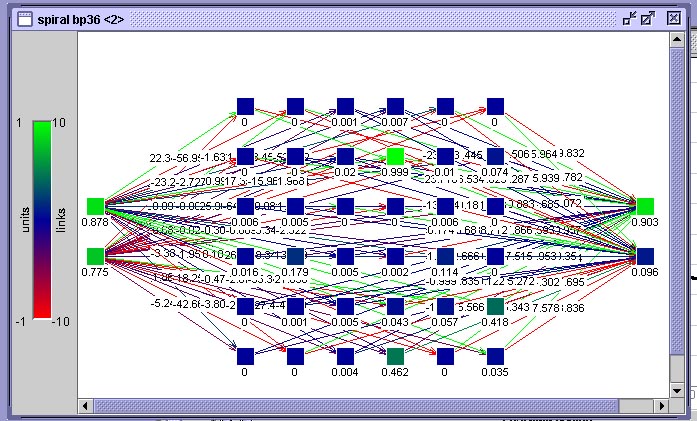
Rede-BP para teste do conjunto espiral dupla mostrada no visualizador de rede do SNNS
A camada da esquerda é a camada de entrada, a camada da direita é a camada de saída. Ambas possuem dois neurônios. Na de entrada são apresentadas as coordenadas x e y do ponto na espiral e na de saída, há um neurônio para cada classe (braço da espiral). O neurônio que apresentar a maior atividade representa a classe resultante da classificação de um ponto apresentado.
A próxima figura representa o gráfico de variação do erro E(w) durante o treinamento desta rede. A abcissa representa o número de épocas (ciclos sobre todos os 360 padrões) e a ordenada o erro global E(w) da rede. Nós interrompemos o treinamento em 42.000 épocas, o que para um conjunto de treinamento de 360 padrões, perfaz 15.120.000 iterações. Observe que o erro se reduz em “saltos”. Isto é comum em métodos de descida em gradiente e significa que o processo encontrou uma “ravina” na paisagem de gradientes e começou a descê-la até encontrar outro “platô”
. 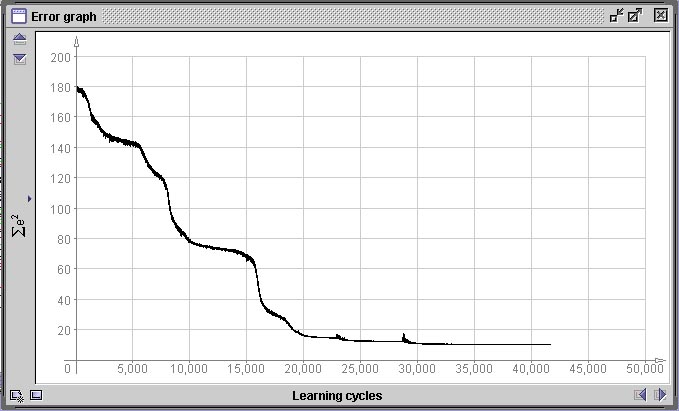
Gráfico do erro global E(w) da rede da figura anterior.
Decidimos abortar o treinamento em 42.000 ciclos pois o erro não apresentou mais redução significativa durante 20.000 ciclos, o que significa que a rede ou encontrou o máximo de fidelidade possível no mapeamento da função que desejamos que aprenda ou então que encontrou um mínimo local na paisagem de erro. Um mínimo local é um pequeno “vale” na paisagem de erro definida por E(w), mas que não contém o menor erro possível. Como as regiões ao redor de um mínimo local são regiões que possuem todas um erro menor e o método de descida em gradiente tenta sempre encontrar um novo conjunto de valores de pesos que reduza o erro e nunca um que aumente, a rede nunca sairá dalí. Mínimos locais são o maior problema que deparamos em métodos de descida em gradiente. Como o estado inicial do sistema é aleatório e a ordem de apresentação dos padrões também, o caminho que leva ao mínimo erro global pode passar por um mínimo local ou não, dependendo do acaso. Quando nos deparamos com um mínimo local onde a rede “encalhou”, a única opção que temos utilizando o algoritmo de rede-BP tradicional é a de reinicializar a mesma e treinar novamente desde o início. Ná próxima figura vemos três situações de gráfico de erro completamente diferentes geradas após 50.000 épocas pela mesmo rede com o mesmo conjunto de dados. Apenas foram geradas inicializações diferentes, porém com os mesmos parâmetros.
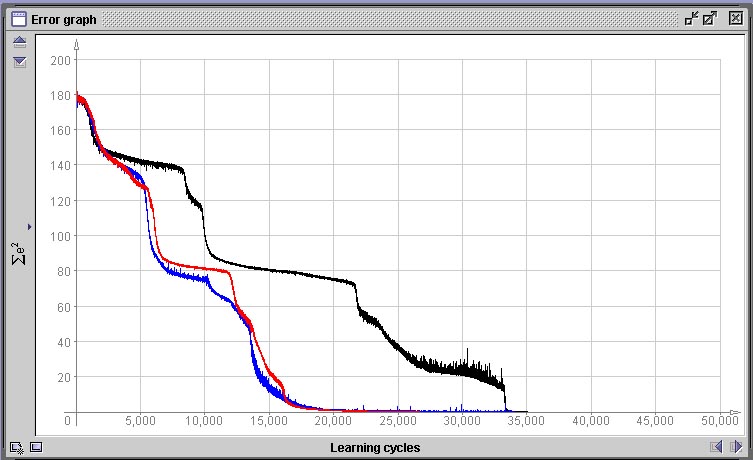
Comparação de variação aleatória de performance de treinamento em dependência da inicialização
Nos três casos acima, apesar da performance de aprendizado ter sido bastante diferente, em nenhum dos três casos a rede encontrou um mínimo local e estacionou em um platô de erro constante. Todas as três redes atingiram um erro próximo de 0.
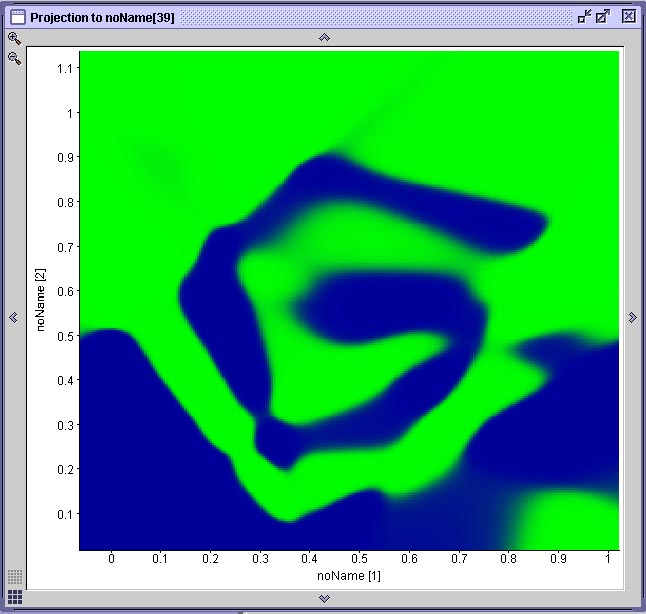
Na figura abaixo vemos o resultado da projeção de duas superfícies de decisão geradas por duas das mostradas anteriormente. Cada projeção é gerada através de uma ferramenta do SNNS que permite associar-se graficamente dois neurônios de entrada a um de saída. O gráfico resultante mostra a ativação do neurônio de saída para todas as possíveis combinações de valores de entrada nos dois neurônios selecionados. No caso específico da espiral dupla, onde existem apenas dois neurônios de entrada e dois neurônios de saída, esta projeção corresponde à superfície de decisão gerada pela rede. Compare este resultado com a performance do algoritmo IBL, observando que cada rede que gerou este resultado teve de ser treinada durante 20 minutos em um computador com 512 MB de RAM e um processador AMD 1800+ e que o algoritmo IBL (1, 2 ou 3) toma uma fração de segundo para realizar a mesma coisa em um computador com essas especificações.
 |
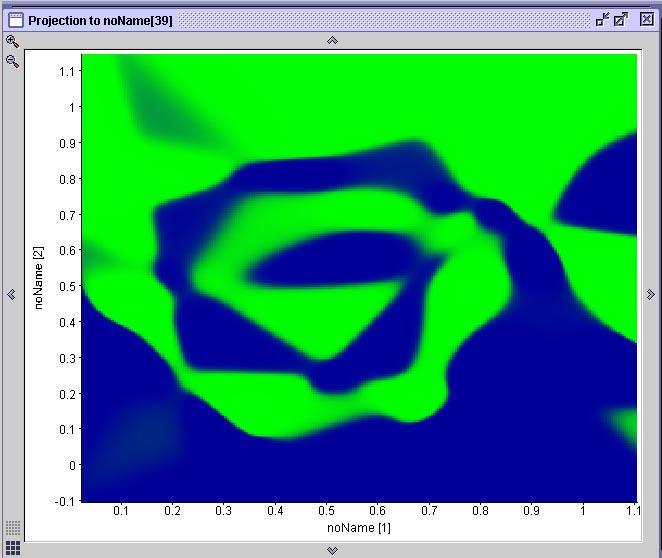 |
Duas projeções das superfícies de decisão geradas pelas redes anteriores
Observe que na rede (A) há uma área mapeada incorretamente. A rede (B) aprendeu a espiral com qualidade aceitável. A rede (A) é a primeira rede neural treinada, cuja treinamento foi interrompido em função de uma mínimo local. Aqui podemos observar que o mínimo local que a rede encontrou a impediu de aprender uma parte do problema, fazendo com que a superfície de decisão ficasse incompleta.
Aprendizado de Conjuntos Intrincados Apresentando Erro
Para termos uma idéia como se comporta uma rede-BP nos casos onde existe algum erro nos conjuntos de dados, retomemos as nossas espirais geradas apresentando desvio aleatório de posição dos dados do conjunto de treinamento de até 15 e de até 30 pixel.
Espirais com erro de até 15 e de até 30 pixel na posição dos pontos
O resultado do treinamento de três redes com o conjunto de dados de treinamento com erro de até 15 pixel pode ser visto abaixo. Observe que a superfície de decisão gerada (mostra a rede cuja curva de treinamento está em preto) é bastante boa. As curvas de treinamento mostram que uma das redes treinadas (curva em azul), além de mostrar um comportamento de aprendizado bastante ruim, com muitas oscilações, provavelmente vai cair em um mínimo local.
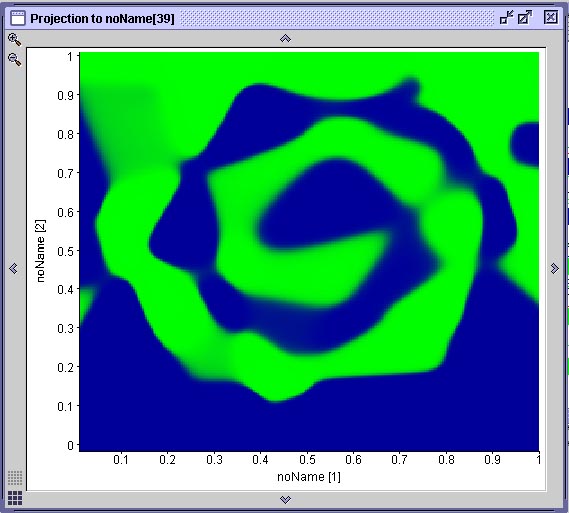 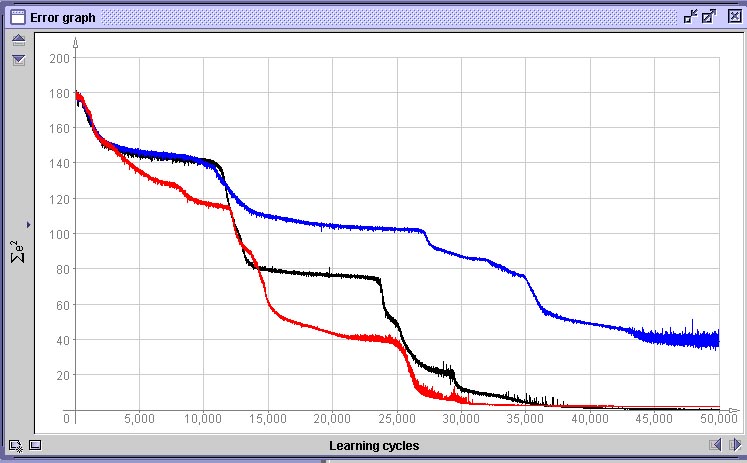 |
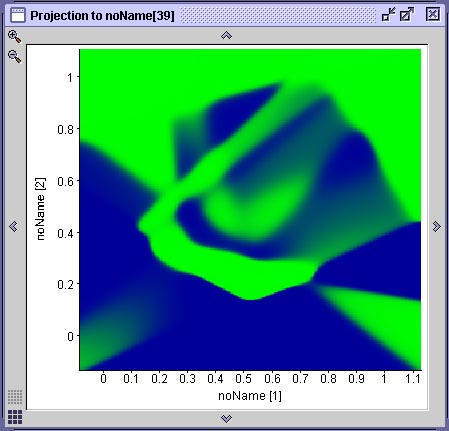
Comparação de 3 redes treinadas com o conjunto com erro de 15 pixelSe utilizarmos o conjunto de treinamento gerado com erro de até 30 pixel, a qualidade do aprendizado deteriora bastante, como vemos na superfície de decisão abaixo. As curvas comparam a performance de uma rede treinada com dados com erro de 30 pixel (vermelho), erro de até 15 pixel e uma treinada com dados sem erro.
 |
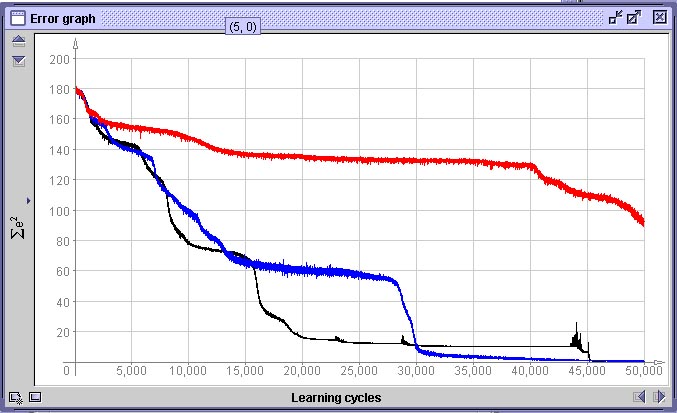 |
Comparação de 3 redes treinadas com o conjuntos com erro diferentesDados:
- Arquivo .PAT em sintaxe SNNS dos 360 pontos da Espiral Dupla para treinamento
- Arquivo .PAT em sintaxe SNNS dos 360 pontos da Espiral Dupla para treinamento (Com Erro 15)
- Arquivo .PAT em sintaxe SNNS dos 360 pontos da Espiral Dupla para treinamento (Com Erro 30)
Uma Aplicação de Reconhecimento de Padrões Simples: Reconhecer CEPs em Cartas
Tarefas que parecem mais complexas do que a classificação de dados sintéticos como o da espiral dupla, são, muitas vezes, bastante mais simples. Um exemplo é o caso do reconhecimento ótico de caracteres impressos.
Suponha um sistema para litura automática do CEP em cartas. O sistema pressupõe que o CEP foi batido à máquina. Nosso exercício aqui pressupõe também que os passos iniciais, onde o CEP deverá ser identificado na carta, recortado da imagem da carta e normalizado para uma mesma resolução (número de pixel) são realizados por um algoritmo que não interessa no momento (vamos vê-los mais tarde no capítulo de processamento de imagens).
Um exemplo de um conjunto de números + hífem impresso por uma máquina de escrever e possíveis CEPs escritos com ela está abaixo.
Para criar um pequeno sistema de OCR (reconhecimento ótico de caracteres) vamos supor que a primeira linha do escaneado na figura anterior será nossa amostra para treinamento. Para preparar esta amostra para que uma rede neural possa aprendê-la temos de primeiramente seguir os seguintes passos:
- Decidir por uma representação. Neste caso vamos escolher representar os valores diretamente através de seus valores de pixel. Como a camada de entrada de uma rede-BP é unidimensional, vamos representar a matriz de uma imagem por linhas, cada linha ao lado da anterior.
- Aumento do contraste. As imagens da amostra (escaneadas com os tons de cinza do papel) são de baixa qualidade. Simplesmente aumentamos o contratste da imagem para tornálos mais visíveis.
- Redução da resolução. Se pretendemos representar cada algarismo pelos seus pixels, não podemos fazer isto numa resolução onde cada algarismo ocupa uma matriz 70×100 ou similar. Temos de realizá-lo de forma simplificada. Fá-lo-emos inicialmente com uma matriz de aproximadamente 10×15.
- Normalização: Como os tipos da máquina de escrever são de tamanho diferente, escolhemos um tamanho-meta e “normalizamos” as imagens para este tamanho. O tamanho-meta será 10×15 pixel, significando 150 neurônios na camada de entrada da rede. Agora tomamos cada número, recortamos exatamente os pixeis não brancos e redimensionamos a imagem resultante para 10×15.
Tudo o que temos de fazer ainda é criar arquivos de dados para treinamento da rede. Nós fizemos um método simples em Smalltalk que lê um arquivo de dados binário e incluios dados em um arquivo ASCII na sintaxe do SNNS. Como entrada para este método usamos um conjunto de dados gerado a partir das imagens acima salvando-as em formato .RAW (só bytes e mais nada) em um editor de figuras. A cada figura carregada neste método, associamos manualmente um valor de saída.
Agora podemos criar uma rede-BP no SNNS com 150 neurônios de entrada, 10 de saída e um número qualquer (no nosso exemplo: 30) na camada intermediária, como na figura abaixo:

Ativação da camada de entrada ao apresentar-se um padrão
Na década de 1960 foi criado um conjunto de caracteres especialmente desenvolvido para ser utilizado com OCR. Ele existiu em várias versões e a versão mais conhecida e utilizada até hoje em muitos locais do mundo onde se pratica OCR em formulário é o fonte OCR-A, mostrado abaixo. Até um perceptron simples deveria ser capaz de reconhecer caracteres em OCR-A sem dificuldade. Você vai realizar este experimento. No seu trabalho você vai, além dos caracteres de máquina de escrever acima, treinar uma rede neural com OCR-A, disponibilizado em 10×15 abaixo. Esta rede neural vai ter várias arquiteturas e uma delas será um perceptron simples, sem camada intermediária. Funciona ?

Exemplo do fonte OCR-A especialmente desenvolvido na década de 1960 para reconhecimento ótico. Na parte de cima da figura repetimos a seqüência de caracteres numéricos representada em um grid de pixels de 10×15 para cada caracter. Nesta resolução foram gerados os dados para a sua rede neural e que estão nos arquivos .raw abaixo.
Outra Aplicação: Determinação Automatizada do Grau de Malignidade (Gradação) de Tumores
aplicada ao exemplo da gradação de tumores do grupo dos astrocitomas/glioblastomas (tumores cerebrais)
 Veja http://www.inf.ufsc.br/~awangenh/pathos.html
Veja http://www.inf.ufsc.br/~awangenh/pathos.html
Trabalhos
Passados em sala de aula.
Dados para os trabalhos:
- Conjunto de arquivos .JPG e .RAW dos números de máquina de escrever normalizados em 10×15
- Conjunto de arquivos .JPG e .RAW dos números em OCR-A normalizados em 10×15 (aqui em .rar)
- Arquivo .PAT em sintaxe SNNS dos números de máquina de escrever para treinamento
- Para os números em OCR-A você mesmo deverá gerar os arquivos .pat a partir dos dados .raw
Breve Comparação entre Redes-BP, redes-RBF e métodos simbólicos utilizando Nearest Neighbour
Nesta seção realizaremos uma breve comparação entre redes-RBF e redes-BP, extraída de [Haykin] e um comentário nosso sobre redes-RBF e sua relação com Nearest Neighbour e métodos que utilizam NN, como IBL*.
As redes-RBF e os perceptrons de múltiplas camadas treinados com algoritmo backpropagation (redes-BP) são ambos exemplos de redes feedforward não lineares treinadas através de aprendizado supervisionado, sendo aproximadores universais. Isto quer dizer, se existe uma função capaz de mapear o conjunto de vetores de entrada no conjunto de vetores de saída (classes) desejado, este mapeamento é garantido ser possível de ser aprendido, dispondo-se de memória e tempo de processamento suficientes.
Esta equivalência garante que sempre existirá uma rede-RBF capaz de reproduzir o comportamente de uma rede-BP específica e vice-versa. As diferenças entre os modelos são as seguintes:
- Uma rede-RBF clássica terá sempre uma única camada interna (hidden layer), enquanto uma rede-BP pode ter várias.
- As redes-BP são homogêneas e todos os neurônios possuem o mesmo modelo, compartilhando a mesma função quaselinear de ativação, não importando em qual camada se encontram. Os neurônios de uma rede-RBF possuem funções de ativação diferentes, sendo que a camada interna possue geralmente uma função gaussiana e a camada de saída uma função linear (que pode ser a identidade). Isto significa que a camada interna de ma rede-RBF é não linear, mas sua camada de saída é linear. No rede-BP todas as camadas são não-lineares.
- A função de ativação dos neurônios da camada interna de uma rede-RBF calcula a distância euclideana entre o vetor de entrada e o centro daquele neurônio. A função de ativação de uma rede-BP calcula o produto interno do vetor de entrada pelo vetor de pesos daquele neurônio.
Como conseqüência do ponto acima, as redes-BP constroem aproximações globais de um único mapeamento de entrada-saída não-linear, aproximando uma função que representa este mapeamento, enquanto que as redes-RBF constroem aproximações locais para mapeamentos de entrada-saída não-lineares utilizando modelos não-lineares com decaimento exponencial (p.ex. funções gaussianas) para este fim.
Em resumo, uma rede-BP tenta encontrar uma única função não-linear capaz de representar o problema sendo treinado, enquanto que uma rede-RBF realiza um conjunto de aproximações locais não-lineares (uma por neurônio interno) baseadas em distância euclideana e delimitadas por uma função gaussiana que sejam linearmente separáveis e possam ser representadas pela função de mapeamento linear implementada entre a camda interna e a camada de saída.
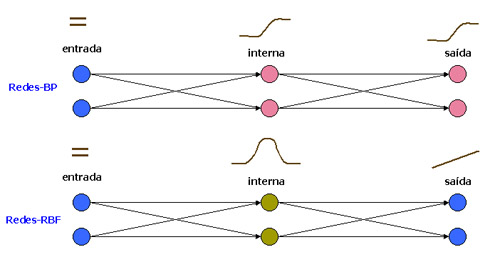
Visão geral da distribuição das funções de ativação em redes-BP e -RBF:
Acima de cada camada está representado o tipo de função de ativação típico.
Considere agora o seguinte:
- Sabemos que métodos utilizando Nearest Neighbour, como os algoritmos da família IBL ou kNN realizam um mapeamento muito parecido com a descrição das redes-RBF dada acima. A diferença está no fato de que não existe uma suavização da distância euclideana através de uma curva gaussiana (ou função similar).
- A não-linearidade que permite ao modelo baseado em NN representar problemas complexos é introduzida pela heurística de limiar móvel dada pela regra de escolha do protótipo mais similar.
- Traduzindo em outras palavras, o modelo utilizado pelo algoritmo IBL, por exemplo, é um mapeamento local não linear porque, apesar da distância euclideana representar um mapeamento linear, o fato de aplicarmos uma decisão binária ao resultado da nossa comparação de distâncias (tomando o protótipo mais próximo) representa uma não-linearidade similar ao de um limiar (threshold).
- Sugerimos que você tome alguns problemas clássicos (espiral dupla, por exemplo) e outros com os quais você esteja familiarizado e realize uma comparação entre a performance de redes-RBF com várias topologias e a performance de vários modelos IBL, como IBL2, IBL3, etc:
- Qual a diferença no tempo de treinamento ?
- Qual a diferença na taxa de erros de classificação ?
- Qual a tolerância a erros ?
- Acreditamos que os resultados que você vai obter vão lhe ensinar bastante sobre reconhecimento de padrões.
Agrupadores: Usando Aprendizado Não Supervisionado para Organizar Padrões
a) como uma forma de abstração dos padrões apresentados, onde associamos cada grupo “descoberto” pelo método a uma classe ou categoria eb) como um classificador auto-organizante, onde podemos utilizar a informação codificada durante o agrupamento dos padrões em categorias como mecanismo de classificação de novos padrões, apresentados em um estágio posterior.
O Modelo de Kohonen e Quantização de Vetores
Consideramos o artigo de Kohonen e Ritter um marco tão importante na história das redes neurais e uma explicação tão perfeita sobre o modelo, que vamos reproduzi-lo aqui na íntegra, através da sua tradução para o Português realizada por Maricy Caregnato e Emerson Fedechen, do CPGCC da UFSC. Esta tradução será entremeada de comentários nossos e de exemplos de reprodução dos experimentos de Kohonen e Ritter com o SNNS.
Os Mapas Auto-Organizantes de Kohonen
Biological Cybernetics, 61, 241-254, Elsevier, Amsterdam, 1989
Tradução: Maricy Caregnato e Emerson Fedechen, CPGCC, UFSC.
Resumo
Hipóteses sobre a representação interna de Elementos da lingüística e estruturas
Categorias e suas relações para representações neurais e lingüísticas
Desde que representações de categorias ocorreram em todas as linguagens, muitos recursos tem estipulado que os elementos semânticos mais profundos de uma linguagem podem ter uma representação fisiológica em um domínio neural; e se eles são independentes de uma história cultural diferente, isso conclui que tais representações devem ser herdadas geneticamente.
Na época que a predisposição genética de elementos de linguagem foi sugerida, não havia mecanismo conhecido que teria explicado as origens das abstrações em informações neurais processada outra então evolue.. Isto não foi desde que a modelagem “redes neurais” alcançasse o nível presente quando pesquisadores começaram a descobrir de propriedades abstratas de representações internas dos sinais de modelos na rede física. Lá existe pelo menos duas classes de modelos com este potencial: a rede backpropagation e a map self-organizing. O encontrado indica que as representações internas de categorias podem ser deriváveis de relações e regras mútuas de um sinal primário ou elementos de dados.
Contudo o propósito deste paper não é afirmar que todas as representações no cérebro biológico somente são adquiridas pelo aprendizado. Os princípios adaptativos discutidos abaixo podem ser considerados como frameworks teóricos, e a primeira faze do aprendizado é a forma mais simples. É totalmente possível que um processo similar esteja trabalhando em um ciclo genético, por outro lado esses mecanismos explícitos são difíceis para imaginar.
Isso agora será próprio para abordar o problema de mapas semânticos auto organizáveis usando dados que contém informações implícitas relatando simples categorias; se mais tarde forem detectados automaticamente , podemos pensar que o passo significante em direção ao processamento lingüístico auto organizável foi feito.
Um aspecto pode ser ainda enfatizado. Isso talvez não seja razoável para procurar por elementos de linguagens no cérebro. A visão mais fundamental é que as funções fisiológicas são esperadas para refletir a organização categórica e não tanto as formas lingüísticas detalhadas.
Exemplos de modelos de redes neurais para representações internas
Mapas de auto organização (características topológicas)
A forma mais genuína de auto organização é o aprendizado competitivo que tem a capacidade de encontrar agrupamentos das informações primárias , eventualmente em modo de organização hierárquica. Em um sistema de características de células sensitivas o aprendizado competitivo significa que um número de células está comparando os mesmos sinais de entrada com seus parâmetros internos , e a célula com o melhor competidor (winner) é então auto ajustada a esta entrada. Desta forma diferentes células aprendem diferentes aspectos da sua entrada , que podem ser considerados como a mais simples forma de abstração.O mapa de auto organização é um adiantado desenvolvimento do aprendizado competitivo em que a célula de melhor entrada também ativa seus vizinhos topográficos na rede para fazer parte no afinamento da mesma entrada. Um acerto, não significa resultado óbvio coletivo , o aprendizado coletivo assume a rede neural como uma falha de duas dimensões. As diferentes células tornam-se ajustados a diferentes entradas em uma moda ordenada , definindo características de sistemas de coordenadas através da rede. Após o aprendizado, cada entrada obtém uma resposta localizada , qual posição no papel reflete a mais importante “coordenada característica”da entrada. Isso corresponde a uma projeção não linear do espaço de entrada na rede que faz a melhor relação de vizinhança entre elementos explícitos geometricamente. Particularmente se os dados são agrupados hierarquicamente , uma representação muito explícita está localizada na mesma estrutura gerada. Enquanto mapas auto organizáveis como foram usados para muitas aplicações para visualizar dados agrupados , muitas possibilidades intrigantes são diretamente possíveis de criar um processo de representação topográfica da semântica de relação não métrica implicando em dados lingüísticos.
As funções de processamento da informação estão localizadas no cérebro? Justificação do modelo.
No final do século IXX, a organização topográfica detalhada do cérebro, especialmente o cortex, já foi deduzível de déficits funcionais e falhas comportamentais que foram induzidas por vários tipos de defeitos causados acidentalmente, adequado para tumores, mal formações , hemorragias ou lesões causadas artificialmente . Uma técnica moderna causa lesões controláveis e reversíveis, é para estimular uma parte em particular na superfície cortical por pequenas correntes elétricas, através disso eventualmente induzem efeitos inibitórios e excitatórios, mas de qualquer forma uma função local assume um distúrbio. Se tal estímulo confinado globalmente então sistematicamente interrompe uma habilidade cognitiva específica tais como objetos, lá existe a menor indicação que o lugar correspondente é essencial para aquela tarefa. Esta técnica foi criticada freqüentemente pelo fato que carrega para todos os estudos nas lesões. Por outro lado uma lesão similar no mesmo lugar sempre causaria a mesma deficiência, e a mesma deficiência nunca foi produzida por um outro tipo de lesão, ela não é logicamente possível usar como dado como uma prova conclusiva para localização; a parte principal da função pode residir em outro lugar, enquanto a lesão pode destruir somente uma conexão do controle vital para ela. Hughlings Jackson já declarou “Para localizar os danos que destroem a fala e para localizar a fala são duas coisas diferentes “
Uma outra forma controlável para a determinação da localização é comprimir quimicamente ou herdar o processo que causa o engatilhamento dos neurônios , ou seja, usar pequenos retalhos embebidos em striquinina. Esta técnica foi usada com sucesso para mapear, isto é, funções sensoriais primárias.
O método mais simples é localizar uma resposta para armazenar o potencial ou encadeamento de impulsos neurais associados com ele. Apesar de desenvolver técnicas multi-eletródo geniais, este método não detectou todas as respostas em uma área desde que o encadeamento neural seja homogêneo , a união faz um neurônio particular ser mais eventual, especilamente de um sensor primário e de áreas associativas , foi feito por várias técnicas registradas eletrofisiológicamente. Evidencias mais conclusivas para localização podem ser obtidas por modernas técnicas imaginárias que mostram diretamente a distribuição espacial da ativação do cérebro associado com a função alcançando uma resolução espacial de alguns milímetros. Os dois métodos principais que são baseados em traçadores radioativos são eles: Positron Emission Tomography(PET), e auto radiografia do cérebro através de conjuntos de colimadores muito pequenos (câmara gama). PET revelam mudanças no uptake oxigênio metabolismo fosfato. O método de câmara gama detecta mudanças diretamente no fluxo sanguíneo cerebral. Os fenômenos correlate com a ativação neural local, mas eles não estão hábeis a seguir rapidamente os fenômenos. Em magnetoencephalography (MEG), o baixo campo magnético causado por respostas neurais é detectado, e por computação desses recursos, as respostas neurais podem ser diretamente ser analisada com razoável rapidez , com uma resolução espacial de junção de milímetros. A principal desvantagem é que somente tais dipoles atuais são detectáveis, as que estão em paralelo na superfície do crânio, isto é, principalmente o silco do córtex que pode ser estudado com este método.
Parece existir uma técnica não ideal que sozinha seria usada para mapear todas as respostas neurais. Ela é necessária para combinar estudos anatômicos, eletrofisiológicos, imaginários e histoquímicos.
Mapas topográficos em Áreas sensoriais
Genericamente, dois tipos de mapas fisiológicos são distinguíveis no cérebro: aqueles que soa claramente ordenados, e aqueles que são quase randomicamente organizados, respectivamente. Mapas que formam uma imagems contínuas ordenada de algumas “superfícies receptivas” podem ser encontradas na visão, e córtices somatosensoriais no cerebelo , e em certo núcleo. A escala local no fator de sublimação desses mapas depende da importância comportamental de sinais particulares , ou seja, imagens de parte foveal da retina , a ponta dos dedos e os lábios são sublimes em relação as outras partes. Há assim um mapeamento “quasiconformal”da “superfície” dentro do cérebro.Também há mais mapas abstratos, ordenados, contínuos em muitas outras áreas sensoriais primárias , tais como o tonotopic ou mapas de freqüência auditiva. Isso é uma característica comum de tais mapas que são confinados para uma área menor, raramente excedendo 5mm de diâmetro, como isso é justificado para usar o modelo dela no qual a rede total é assumida homogeneamente estruturada. Sobre uma área , um mapeamento espacialmente ordenado ao longo de uma ou duas dimensões de atributos importantes de um sinal sensorial é usualmente discernível.
Fisiologistas também usam a palavra “mapa” para respostas não ordenadas para estímulos sensoriais contanto que estes sejam localizáveis espacialmente, até se eles forem randomicamente dispersos em cima de uma área de vários centímetros quadrados e muitos tipos diferentes de respostas forem encontrados na mesma área. Respostas visuais mais complexas encontradas em níveis mais altos são mapeadas desta forma: por instância, células foram detectadas respondendo seletivamente a faces.
Evidências para localização de função lingüística :
Foi conhecido no início do século que a afasia sensorial é causada por lesão nas parte superior e posterior do lobo temporal no cérebro chamada área de Wernicke; mas com técnicas modernas de tratamento de imagem somente uma localização muito mal feita de funções da linguagem tem sido possível. Praticamente toda a função sistemática de alta resolução mapeada foi feita por um método de simulação.
É muito mais difícil localizar lingüísticas em funções semânticas no cérebro do que para mapear as áreas sensoriais primárias. Primeiro, ele ainda não esta claro para quais aspectos da linguagem as dimensões características podem corresponder. Segundo, como foi notado recentemente como um mapeamento pode ser disperso.Terceiro, resposta para elementos lingüísticos podem somente ocorrer dentro “time windows”. Quarto, as técnicas experimentais usadas em animais estudados sendo usualmente evasivos, não podem ser aplicados a seres humanos, a menos que exista indicação de uma operação cirúrgica. Contudo, o significado entre evidencias experimentais já é avaliável suportando a visão do grau mais alto da localização nas funções da linguagem.
PET da imagem tem revelado que durante a tarefa de processar simples palavras , diversos lugares de cortes corticais são ativados simultaneamente. Estes não estão todos localizados na área de Wernicke :algumas partes do lobo frontal e as áreas associativas podem mostrar respostas simultaneamente também, especialmente em locais obviamente associados com percepção visual e auditiva , articulação e planejamento de tarefas.
Ao invés de estudar representações internas , localização de lugares relacionados a processos semânticos precisam de melhor resolução ao invés de um milímetro tão difícil de registrar mesmo por estímulos de mapas, entretanto este método não pode detectar algum pico de atividade temporal, isso pode apenas produzir bloqueio temporário reversível do processo em uma região confinada a um milímetro quadrado. Estimulações repetidas da mesma área causa uma espécie de deficiência temporária , isto é, erros em nomear objetos, ou dificuldade em recolecionar da memória de padrões verbais curtas. Contudo, a estimulação de algumas outra áreas apenas 5mm já separados podem induzir tipos completamente diferentes de deficiência ou sem efeito algum. Adicionalmente estes são casos de pacientes bilíngües onde nomeados pelo mesmo objeto e prejudicado em apenas uma das linguagens dependendo da área que está sendo estimilada. Isso parece como se a função da linguagem fosse organizada como um mosaico de módulos localizados .
Outra evidência indireta para um mapeamento estruturado está disponível em diversos casos nas deficiências selecionadas como resultado de pancadas ou cérebros feridos. Exemplos incluem deficiências no uso de palavras concretas por abstratas , inamimado por animado ou deixando objetos e comida contra palavras animadas. Lá existe relatório bem documentado em impairements seletivos relatando quais subcategorias como objetos internos , partes do corpo, frutas, vegetais.
Análise de qual informação tem direcionado a conclusão que existe módulos separados no cérebro por uma “palavra lexicamente visual” e a palavra lexicamente fonética para reconhecimento da palavra em semântica léxica para o significado da palavra como uma saída léxica para palavras articuladas, respectivamente cada um desses módulos pode ser independentemente falho.
As falhas categoricamente relatadas acima parecem relatar danos causado seletivamente para a “léxica semântica “. Estas observações não podem prover evidências conclusivas para a localização de classes semânticas sem a léxica, porque em todos esses casos não foi possível avaliar a extensão espacial precisamente no tecido afetado no cérebro. Nonetheles isso parece justificado para aquele estado de falha seletiva em que um grande número de casos, seria muito difícil explicar se a organização semântica aparente da observação não estivasse em alguma forma ponderada no layout espacial do sistema.
Representação de dados topologicamente relacionados em um mapa auto organizável
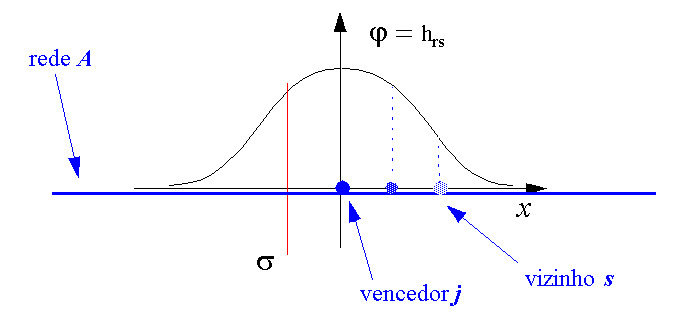
Para a eficiência do processo e conveniência matemática, todos os vetores de entrada são sempre normalizados para tamanho único, considerando que o wr não precisa ser normalizado explicitamente no processo , cedo ou tarde o processo os normalizará automaticamente. Os neurônios estão arranjados em uma grade bi-dimensional, e cada neurônio está rotulado pela sua grade bi-dimensional de posição r. O grupo de neurônios excitados é escolhido para estar centralizado no neurônio s para que x. ws seja o máximo. Esta forma e extensão são descritas por uma função hrs , cujo valor é a excitação do neurônio r se o centro do grupo estiver em s. Esta função pode ser constante para todo o r em uma “zona de vizinhança” em torno de s e zero, como em uma simulação presente em que são supostas para descrever o mapeamento mais natural. Neste caso hrs será o maior em r=s e declínio para zero com distância decrementada ||r-s||. A melhor modelagem realista escolhida para hrs é:
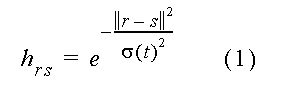
|
|
Os ajustes correspondentes para a entrada X devem ser dados por:
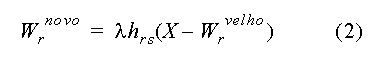
A equação (2) pode ser justificada assumindo a tradicional lei de Hebb para modificações sinápticas, e um processo adicional “active” não linear de esquecimento para a força sináptica. A equação (2) foi desejada propriamente de algumas adaptações de confinamento para a vizinhança do neurônio s e responde melhor ao x.
Mapas de auto organização semântica
O modelo básico do sistema para mapas simbólicos aceita cada dado do vetor x como uma concatenação de dois (ou mais) campos, um especificando o código simbólico, denotado por xb e o outro, o conjunto de atributos, denotado por xa, respectivamente.
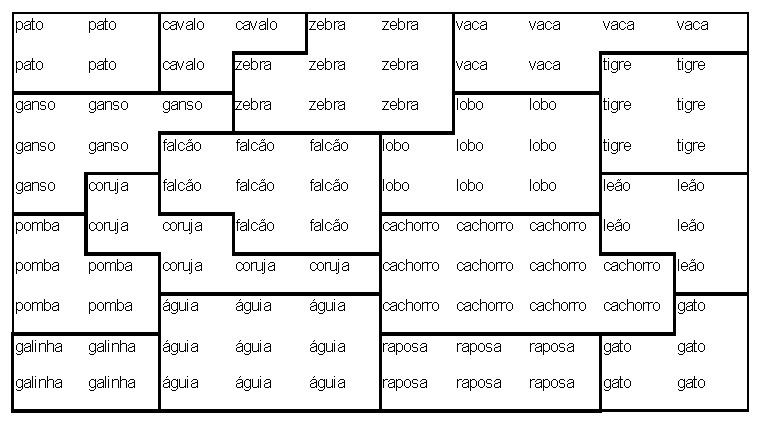
A seguir, nós vamos pegar cada coluna para o campo atributo xa do animal indicado no topo. O próprio nome do animal não pertence a xa mas ao invés disso especifica a parte do símbolo xs do animal. Selecionar o código do símbolo pode ser feito de uma varidade de formas. Entretanto, nós agora queremos ter certeza que o código dos símbolos indiquem alguma informação sobre similaridades entre os itens. Daqui nós escolhemos para a parte simbólica do k-th animal um vetor d-dimensional, o qual k-th componente tem um valor fixo de a, e dos quais componentes remanescentes são zeros. Este d é o número de itens (d = 16 em nosso exemplo). Para esta escolha, a distância métrica entre dois vetores xs é o mesmo, irrespectivo dos símbolos codificados. O parâmetro a pode ser interpretado como medindo a “intensidade” de entrada dos campos simbólicos e isso determina a realtiva influência da parte simbólica comparada com a parte atributo. Como nós procuramos o último que irá predominar, nós escolhemos um valor para a = 0.2 para nossa simulação. Combinando xa e xs de acordo com (3), cada animal foi codificado por um 29-dim vetor de dados x = [xs, xa]t (*elevado a t*). Finalmente cada vetor de dado foi normalizado a um único tamanho. Embora isso é apenas um significado técnico para garantir uma boa estabilidade no processo de auto-organização, sua contraparte biológica poderá ser intensificada a normalização dos padrões de atividade de entrada.
|
|
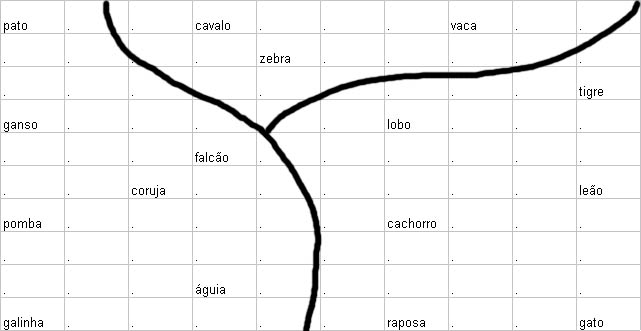
Os membros do conjunto de dados assim obtidos foram apresentados iterativelmente e em uma ordem randomica para uma rede planar de 10 x 10 neuronios ´sujeita a um processo de adaptação descrito a seguir. A conecção inicial força entre os neurônios e seus n = 29 linhas de entrada onde são escolhidos os pequenos valores randomicos. i. e. nenhuma ordem prioritária foi imposta. Entretanto depois de um processo de 2000 apresentações, cada “célula” torna-se mais ou menos responsável por uma das combinações de atributos de ocorrência e simultâneamente para um dos nomes de animais também. Se nóes testarmos agora qual célula dá a resposta mais forte se apenas o nome do animal é apresentado como dado de entrada (i.e. x =[xs,0]t (*elevado a t*), nós obtemos o mapa mostrado na fig. 3.27 (os pontos indicam neurônios com respostas fracas)
Isto é altamente aparente que a ordem espacial das respostas foi capturada a essencial “família de relacionamentos” entre os animais. Células respondendo para, e.g. “birds” ocupam a parte esquerda da rede, “hunters” como também “tiger”, “lion” e “cat” recolhem para a direita, mais “peacefull” espécies como “zebra”, “horse”,e “cow” agregam ao meio superior. Dentro de cada conjunto, um novo agrupamento de acordo com a similaridade é discernido. A fig. 3 mostra o resultado de um “traçado simulado da penetração do eletrodo” para a mesma rede. Ela difere da fig. 2 em que agora cada célula tem sido marcada pelo símbolo que é seu melhor estímulo, i. e., extrai a melhor resposta para aquela célula. Isto faz o parcelamento do “território neural” em domínios específicos para estes itens visíveis de entrada. Hierarquia deste modo é representada por domínios aninhados. A classe geral (e.g. “bird”) ocupa um largo território, no qual ele mesmo é diferenciado em subdomínios aninhados, correspondendo a mais itens especializados (“owl”,”duck”, “hen”, etc.). Embora fortemente idealizado, este resultado é muito sugestivo de como o sistema de auto-organização para guiar espacialmente a formação de traços de memória em tal maneira que seu layout físico final forma uma imagem direta da hierarquia do mais importante “conceito de relacionamentos”.
O resultado da realização de uma simulação no SNNS utilizando estes dados pode ser vista na figura abaixo. Na Figura 3.30.é mostrada a ativação da rede após apresentação apenas da parte simbólica do padrão de número 13 (leão). Aqui foi utilizada uma rede de Kohonen de 10×10 com uma camada de entrada de 29 neurônios, como descrito no experimento. Observe a atividade de neurônios agrupada em um cluster em torno de um neurônio com ativação mais forte.
 |
Dados do Experimento
Para você repetir este experimento em casa estamos disponibilizando aqui os dados para treinamento e teste da rede descrita acima.
- Arquivo de padrões sintaxe SNNS com os dados originais
- Arquivo de padrões sintaxe SNNS com os dados com a parte de atributos atenuada
- Arquivo de padrões sintaxe SNNS para teste contendo apenas os dados da parte simbólica do vetor
- Arquivo com Planilha MS-Excel com todos os dados (para você usar com outros simuladores)
|
|
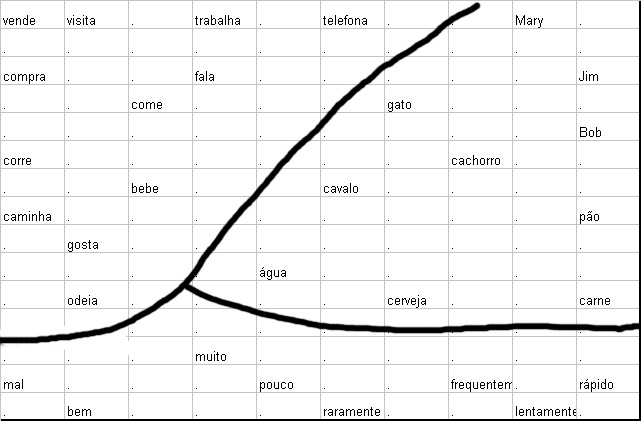
Para a nossa demonstração, nós usamos um conjunto de 3 sequências de palavras randomicamente geradas construídas do vocabulário da Fig. 4 a. O vocabulário contém nomes, verbos e advérbios, e cada classe contém várias subdivisões, como nome de pessoas, animais e objetos inanimados em uma categoria de nomes. Essas distinções são em parte de uma gramática, em parte da semântica natural . De qualquer forma, por razões discutidas na seção 4.1, eles mostraram não ser discerníveis de um código de palavras próprias mas apenas de um contexto de onde as palavras são usadas. Em linguagem natural, como um contexto poderia conter uma rica variedade de experiências sensoriais. Nesta demonstração muito limitada, entretanto, nós poderemos apenas pegar no cliente o contexto fornecido pelo ambiente textual imediatamente adjacente de cada palavra corrente. Isso irá retornar que mesmo este contexto extremamente restrito será suficiente para fazer saber alguma estrutura semântica interessante. É claro que isto requer que cada sentença não seja totalmente randomica, mas obedeça algumas últimas regras rudimentares de gramática e semântica com exatidão. Isto é assegurado por restringir a seleção randomica a um conjunto de 39 padrões de sentenças “legais” apenas. Cada padrão é um trio de números da figura 4b. Uma sentença é construída pela escolha de uma tripla e substituindo cada número por uma das palavras com o mesmo número na fig. 4.a. Este resultado é um total de 498 diferentes sentenças de palavras triplas, alguns dos quais são dados na fig 4c. (Se aquelas indicações são verdadeiras ou não não nos interessa: nós estamos apenas interessados exatidão semântica).
Nesta demonstração muito simples, supôs-se que o contexto de uma palavra seria suficientemente definida pelo par formado pelos seus predecessores e sucessores imediatos. (Para ter tais pares também para a primeira e última palavra da sentença, nós decidimos que as sentenças serão concatenadas em uma ordem randômica da sua produção.) Para o vocabulário de 30 palavras na fig 4a nós poderíamos ter procedido como na seção 4.1 e representado cada para por um vetor de 60-dim com dois não-zeros de entrada. Para uma codificação mais otimizada, de qualquer forma, como explicado mais detalhadamente no apêndice I, nós assumimos para cada palavra, um vetor randômico 7-dim de tamanho único, escolhido fora do conjunto para cada palavra independentemente para uma distribuição probabilística isotropica. Daqui cada par predecessor/sucessor foi representado por um codigo vetorial de 14-dim.
Isso aconteceu em todos os nossos experimentos computacionais que preferencialmente demos atenção para cada cláusula separadamente, uma estratégia de aprendizagem muito mais eficiente foi considerar cada palavra neste contexto médio sob um conjunto de cláusulas possíveis, antes apresentando isso ao algoritmo de aprendizado. O (significado) contexto de uma palavra foi deste modo definido primeiramente como média sobre 10.000 sentenças de todos os códigos vetoriais de pares predecessor/sucessor cercando essa palavra. O trigésimo resultado da 14-dim “contexto médio de palavras”, normalizada a um único comprimento, assumiu uma regra similar como campo de atributos xa na simulação prévia. Cada “campo de atributo” foi combinado com um 7-dim “campo simbólico”, xs consistindo em um código vetorial para a sua palavra, mas adequada ao comprimento a. Neste momento, o uso do vetor de código randômico quase garantiu que o campo simbólico xs não saiba nenuma informação sobre relacionamentos de similaridade entre as palavras. Como antes, o parâmetro a determinou a influência relativa da parte simbólica em comparação a parte contextual e teria o conjunto de a = 0.2.
|
|
Para esse experimento uma grade planar de 10 x 15 neurônios formais seriam usados. Como antes, cada neurônio inicialmente faria apenas conecções randômicas fracas ao n = 21 linhas de entrada do sistema, então novamente, nenhuma ordem inicial seria apresentada.
Depois de 2000 apresentações de entrada as respostas dos neurônios das partes simbólicas somente seriam testadas. Na fig. 5, o quadro simbólico foi escrito para mostrar o local onde o sinal do símbolo x = [xs,0]t (*elevado a T*) deu a resposta do máximo. Nós claramente vemos que os contextos tem “canalizado” os itens das palavras às posições de memória das quais refletem as relações gramáticas e semânticas. Palavras de mesmo tipo, i. e. nomes, verbos e advérbios tem segregado em separado, grandes domínios.
O “mapa semântico” obtido em uma rede de 10 x15 células depois de 2000 representações de pares de palavras-contexto derivados de 10.000 sentenças randômicas do tipo mostrado na fig. 4c. Nomes, verbos e advérbios são segregados dentro de diferentes domínios. Dentro de cada domínio um agrupamento adicional concorda com aspectos do significado como discernimento.
Cada um desses domínios é mais adiante subdividido por similaridade no nível de semântica. Por instância, nomes de pessoas e animais tendem a ser aglomerados em subdomínios em comum “domínio do substântivo”, refletindo em co-ocorrências diferentes com, e.g. verbos como “correr” e “telefonar”. Advérbios com significado oposto tendem a ser particularmente fechados juntos, como o oposto deles significa assegurar a eles o uso máximo do espaço comum. O agrupamento de verbos indicam diferenças nos caminhos, eles podem co-ocorrer com advérbios, pessoas, animais e objetos não animados como e.g. “comida”.
Figura 6 mostra o resultado de um outro experimento, baseado no mesmo vocabulário e mesmo padrão de sentença como antes. De qualquer forma, nesta simulação o contexto de uma palavra foi restrita apenas ao seu predecessor. (O contexto agora consiste de um vetor de 7-dim). Mesmo isto sendo muito limitado, provou como sendo suficiente para produzir um mapa com aproximadamente similar as propriedades como na fig 5. Isto mostra que as regularidades apresentadas são um tanto robustas para trocas nos detalhes da codificação tão grande quanto o contexto capturar uma quantidade suficiente da estrutura lógica subjacente.
|
|
Pode-se discutir que a estrutura resultante no mapa tinha sido artificialmente criada por uma escolha pre-planejada da sequência de padrões reservadas na entrada. De qualquer forma, isso é facilmente verificado nos padrões da fig. 4b quase que completamente até a exaustão das possibilidade de combinação das palavras da fig 4a em uma semanticidade bem formada de sentenças de 3 palavras (um leitor astuto pode verificar alguns “casos de linha semânticas” não cobertas, como “dog eats cat”). Isto pode tornar isso claro que todos padrões de sentenças selecionados estavam realmente determinados pelas restrições inerentes na semanticidade correta usada pelas palavras, e não vice-versa. Além disso, uma porcentagem significativa das palavras vizinhas estendem-se através das bordas das sentenças randomicamente concatenadas. Nesta concatenação foi irrestrita, tais vizinhos foram largamente irrelacionados a estrutura semântica e gramatical das sentenças, e constituíram um tipo de “ruído” no decorrer do processo. Isso é importante observar que este ruído não disfarça as regularidades se não forem apresentadas nas cláusulas.
De qualquer forma, o que importante observar está exatamente aqui. Alguma semântica realística de mapas cerebrais, precisariam de um modelo hierárquico probabilístico muito mais complicado. A finalidade de um simples modelo artificial usado neste trabalho foi apenas demostrar o potencial de um processo auto organizacional par formar mapas abstratos. Em particular, os resultados da simulação, como está, não poderia ser usado como referência para comparação topográfica direta com áreas do cérebro. Como uma comparação entre a fig. 5 e fig.6 mostram, existem muitos caminhos quase equivalentes, nos quais um conjuntos de relacionamentos de similaridades podem ser apresentados no mapa. Consequentemente os mapas gerados pelo modelo não são únicos, a menos que restrições adicionais, como e.g. condições limiares ou alguma ordem inicial grosseria for imposta. Estes podem então inicialmente “polarizar” o sistema que então converge a um outro único mapa.
Discussão: Kohonen é um Modelo Biologicamente Plausível ?
Na primeira simulação nós usamos inicialmente atributos explicitos, deste modo assumindo que algum mecanismo neural já tinha gerado-os. A filosofia subjacente do nosso trabalho é que uma tendência auto-organizadora similar poderia existir em todos os níveis de processamento; ilustrando isto, de qualquer forma, é apenas possível se os sinais tem algum significado para nós.
O termo “mapa semântico” usado neste trabalho, não é ainda referido a “compreensão mais elevada da palavra”; palavras estão apenas sendo agrupadas conforme o seu contexto local. Devido a grande correlação entre contexto local e significado da palavra, entretanto isto aproxima a ordenação semântica encontrada na linguagem natural, o qual presumidamente não pode ainda ser generalizada em cada fase aprendida. Isto é uma questão intrigante se algum estágio de processamento subsequente poderá criar um ordenamento que reflete significados de um nível mais elevado – dos quais poderá facilitar totalmente o entendimento da significado das palavras – por algum tipo de interação do basico processo de auto-organização.
Nosso modelo enfatiza a regra do arranjo espacial de neurônios, um aspecto apenas considerado em muitas poucas abordagens modeladas. Entretanto nós não gostamos de dar a impressão que nós nos opomos a visão de redes neurais como sistemas distribuídos. As interconecções massivas responsáveis pela interação lateral tão bem como os engramas relacionando para a memória associativa são certamente disseminado sobre uma grande área da rede.
Em outra mão, isto mostra-se inevitável que alguma tarefa de processamento complexo precisa algum tipo de segregação de informação em partes separadas, e localização do mais robusto e eficiente caminho para encontrar esta meta. Os mapas semânticos oferecem um mecanismo eficiente para gerar uma segregação significativa de informação simbólica uniforme em um nível razoavelmente alto de semânticas, e eles tem qualidade mais recente de ser o único baseado em aprendizado não-supervisionado. Se nós ainda necessitarmos considerar um timing relativo de sinais. (cf. von der Malsburg and Bienenstock 1986) remanescem o mais recente objetivo do estudo.
Existem outras novas razões não para negligenciar os arranjos espaciais das unidades de processamento. Por instância, a anatomia dos conjuntos de circuitos neurais restringem a realização da conectividade entre unidades. Mais a fundo, sinais cerebrais nãos e apoiam unicamente em transmissão de sinais axonais emitidos em distâncias selecionáveis, mas também emprega difusão de neurotransmissores e neuromoduladores, em todas semelhanças, estas restrições poderiam limitar a implementação de muitos mecanismos computacionais, a menos que este obstáculo esteja aliviada pela eficiente organização espacial oferecida pelos mapas.
De um ponto de vista hardware, se isto fosse esperado que a minimização dos custos de conectividade poderia fortalecer este tipo de design de rede neural. Isto poderia dar um indício porque uma organização topográfica é tão difundida no cérebro. Outros argumentos para localização são que a segregação espacial de representações fazem então mais lógica, pela redução de etapas para a sua inferência mútua, e logicamente de itens simbolicos similares, sendo espacialmente adjacentes, podem invocar um outro associativamente, como expressado nas leis clássicas de associação.
Uma outra observação pode ser necessária. Nossas simulações não poderão ser pegas como uma sugestão que cada palavra é representada por uma então chamada “célula mãe” no cérebro. Cada palavra é um pedaço complexo de informação provavelmente redundante codificada por uma população neuronal inteira (e várias vezes em separado “lexica”, cf. 2.4). Tudo em um grande modelo idealizado usado em nossas simulações, isto não é um simples neurônio mas um subconjunto inteiro de células, cercar o mais responsável deles, que pega o mais adequado a palavra (cf. fig 3). Estes subconjuntos podem então ser engajados em novos processamentos, não capturado pelo modelo básico. O número de células atribuídas a cada subconjunto também depende da frequência das ocorrências das palavras. Isto é análoga ao caso que a frequência de ocorrência de estímulos determina o fator local ampliado em um mapa sensorial (Kohonen op. Cit., Ritter and Schulten 1986). Similarmente palavras frequentes poderiam recrutar células de um grande território neural e ser mais redundantemente representado. Como consequência, as mais frequentes palavras poderão ser menos suscetíveis aos danos locais. Esta complies com observações empíricas nos pacientes do curso, por meio do que as palavras familiares tem mais chances de sobreviver que as raras.
Finalmente, nós gostaríamos de apresentar um noção filosófica intrigante. Como indicado anteriormente, existem vária evidências biológicas e justificações teóricas para o funcionamento do cérebro, requisitando representação de seus dados de entrada por significativas partes processadas em localizações separadas espacialmente. A idéia sobre categorias fundamentais postuladas para a interpretação e entendimento do mundo mais obviamente levanta da formação prioritária de cada representação no próprio mundo biológico do cérebro.
Variação da Função de Vizinhança durante o Treinamento
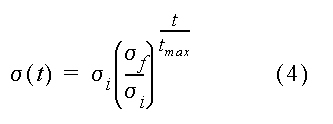
O que aprende uma Rede de Kohonen ?
- uma Rede de Kohonen é inspirada na forma como se supõe que redes neurais naturais aprendem e
- o modelo originou-se a partir das pesquisas anteriores de Teuvo Kohonen em Análise de Componentes Principais e Quantização de Vetores.
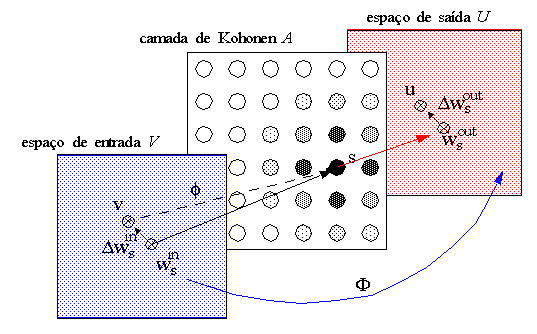
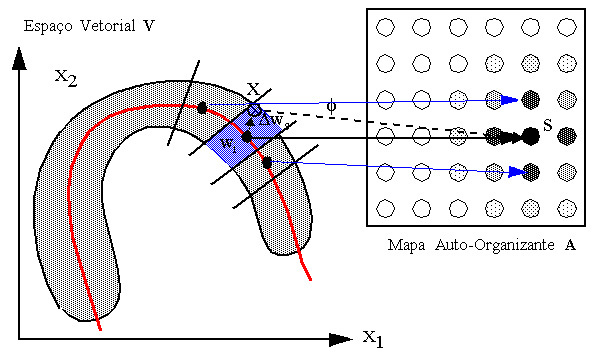
O espaço vetorial V é um espaço qualquer com a dimensionalidade do número de variáveis de um padrão X desse espaço. O vetor de pesos ws do neurônio vencedor S pertencente a A representa uma aproximação da função de mapeamento f que associa pontos do espaço vetorial V a neurônios em A. D ws é o erro dessa aproximação representado no espaço vetorial V.
Com isso, vimos como ocorre o mapeamento de entre o espaço vetorial e o espaço do Mapa Auto-Organizante da rede de Kohonen.
Supondo agora, que os dados em V possuem uma distribuição d qualquer, como é gerada a função de mapeamento f de forma a refletir esta distribuição ?
Qualidades Matemáticas do Modelo de Kohonen
 |
O que uma rede de Kohonen representa após o aprendizado pode ser considerado como uma generalização dessa idéia.
Se nós observarmos uma distribuição de dados representando, por exemplo, todos os pares de valores de duas variáveis x1 e x2 que pertençam à categoria cj, poderemos ter um scatter plot como mostrado em (a) ou em (b) na , dependendo de como os dados se distribuem:
O problema de uma representação deste tipo ocorre quando temos uma distribuição de dados como em (b). Numa situação como essa, o centro da distribuição é um ponto em V que não pertence à distribuição e o eixo principal da distribuição é uma descrição muito pobre e falha do real comportamento desta. É o caso de distribuições de dados com tendências não-lineares, que nós já abordamos no capítulo 1, quando falamos de Nearest Neighbour.
Para representarmos adequadamente uma distribuição de dados como a representada em (b) necessitamos de uma representação não-linear da distribuição, dada por uma curva principal da distribuição, como é mostrado na
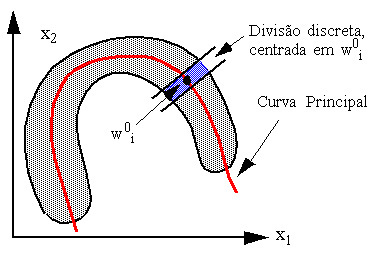 |
O cálculo exato de uma curva principal, porém, pode ser um processo matemático extremamente custoso, envolvendo interpolação polinomial ou outra técnica.
Quando discutimos Nearest Neighbour, no capítulo 1, e algoritmos que o utilizam, como IBL, no capítulo 2, vimos que existe a possibilidade de se aproximar um mapeamento de uma distribuição deste tipo através da divisão desta área curva em pedaços discretos, representados através de um conjunto de protótipos w0i. Isto está muito bem exemplificado pela facilidade com que IBL representa o problem ada espiral exatamente implementando esta técnica. Para gerarmos um conjunto de protótipos w0i deste tipo, porém, é necessário que a distribuição seja conhecida. Isto é fácil, quando temos, de antemão, associada a cada padrão, a sua categoria. Mas como proceder quando não conhecemos a distribuição dos dados nem quais classes existem ?
É aqui que a utilização de Redes de Kohonen se torna interessante: Helge Ritter demonstrou que uma rede de Kohonen aprende exatamente uma representação não linear discretizada deste tipo, sem necessidade de que se forneça de antemão as classes a que pertence cada padrão, realizando uma espécie de Análise Fatorial Não-Linear Discretizada. O resultado do processo de aprendizado, quando a convergência ocorreu adequadamente, é um mapeamento de subconjuntos da distribuição de dados a neurônios específicos da Rede A, que passam a fungir como protótipos para esses subconjuntos. Regiões vizinhas da distribuição são mapeadas para neurônios vizinhos no mapa de Kohonen A. O mecanismo de escolha do vencedor, similar a idéia do Nearest Neighbour, é o que garantre a não-linearidade da capacidade de representação da rede depois de treinada, agindo como uma função limiar, intrinsecamente não-linear, que determina as fronteiras entre cada subárea (subvolume) da distribuição mapeada. Isto pode ser visto na figura abaixo, onde uma classe é representada por um agrupamento (cluster) de neruônios em torno do vencedor S. O vencedor S representa com a maior aproximação o padrão X apresentado à rede..
 |
Explorando Dados Agrupados em Redes
O que aprende uma Rede de Kohonen ?
Vimos até agora que:
- uma Rede de Kohonen é inspirada na forma como se supõe que redes neurais naturais aprendem e
- o modelo originou-se a partir das pesquisas anteriores de Teuvo Kohonen em Análise de Componentes Principais e Quantização de Vetores.
Para fundamentar uma aplicação na prática de Redes de Kohonen como um mecanismo para o aprendizado auto-organizante de padrões e seu posterior uso para classificação de padrões, é importante analisarmos a capacidade representacional e a forma de representação da informação em um Mapa Auto-Organizante.Na prática, uma rede de Kohonen toma um conjunto de dados em um espaço de dados V qualquer e os representa de forma discretizada através de um neurônio (e eventualmente sua vizinhança) no espaço de um Mapa Auto-Organizante A. Esta transformação de um espaço de representação para outro é denominada mapeamento f, podendo ser representada por:
![]()
A condição para que este mapeamento seja uma boa representação do espaço vetorial é que:
![]()
onde W é um vetor de pesos da rede A. Este mapeamento está ilustrado na Figura abaixo:
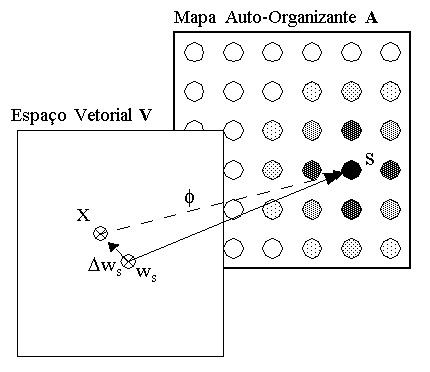
O espaço vetorial V é um espaço qualquer com a dimensionalidade do número de variáveis de um padrão X desse espaço. O vetor de pesos ws do neurônio vencedor S pertencente a A representa uma aproximação da função de mapeamento f que associa pontos do espaço vetorial V a neurônios em A. Dws é o erro dessa aproximação representado no espaço vetorial V.
Com isso, vimos como ocorre o mapeamento de entre o espaço vetorial e o espaço do Mapa Auto-Organizante da rede de Kohonen.
Supondo agora, que os dados em V possuem uma distribuição d qualquer, como é gerada a função de mapeamento f de forma a refletir esta distribuição ?
Qualidades Matemáticas do Modelo de Kohonen
Existem várias interpretações matemáticas da forma como uma rede de Kohonen aprende e de como devemos interpretar o mapeamento f gerado após o aprendizado da rede. Helge Ritter em sua tese de doutorado (Univ. de Munique, 1988) analisou em detalhe ambos. Nós vamos reproduzir aqui, omitindo os detalhes matemáticos, a sua interpretação da representação.
O conceito básico de representação em uma rede de Kohonen baseia-se na idéia de Componentes Principais. A Análise de Componentes Principais é uma técnica de análise de distribuição de dados onde se procura encontrar vetores de referência que representem de uma forma mais ou menos adequada conjuntos de vetores de uma distribuição de dados. Possui utilidade em mineração de dados e para decifrar códigos baseados em índices. A figura abaixo dá um exemplo de três vetores de referência miencontrados para aproximar uma distribuição de dados dividida em grupos.
Figura: Representação de agrupamentos de dados expressando uma função x(t) em um espaço n-dimensional qualquer através de vetores de referência mi

O que uma rede de Kohonen representa após o aprendizado pode ser considerado como uma generalização dessa idéia.
Se nós observarmos uma distribuição de dados representando, por exemplo, todos os pares de valores de duas variáveis x1 e x2 que pertençam à categoria cj, poderemos ter um scatter plot como mostrado em (a) ou em (b) na figura abaixo, dependendo de como os dados se distribuem
Figura: Duas distribuições de dados e suas componentes principais
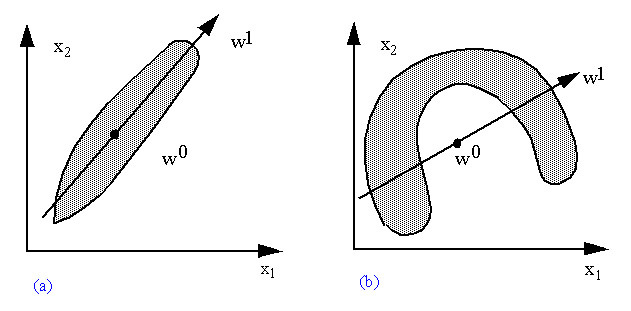
Podemos representar a componente principal desta distribuição de dados através de um único ponto w0 no espaço vetorial, que representará exatamente o “centro de massa” da distribuição, ou através de um vetor w1 que representa o “eixo principal” da distribuição, indicando a sua tendência. Isto pode ser realizado através de várias técnicas estatíticas, entre outras pela Análise Fatorial, utilizada quando a nossa distribuição de dados representa várias classes.
| Nota 1: Se a distribuição é conhecida, podemos calcular w0 usando exatamente o método de cálculo do centro de massa da Física, atribuindo uma massa qualquer, não nula, a cada um dos pontos do conjunto. |
| Nota 2: Das mesma forma, se a distribuição é conhecida, podemos utilizar o método de cálculo do eixo de massa principal da Física para obter w1. |
O problema de uma representação deste tipo ocorre quando temos uma distribuição de dados como em (b). Numa situação como essa, o centro da distribuição é um ponto em V que não pertence à distribuição e o eixo principal da distribuição é uma descrição muito pobre e falha do real comportamento desta. É o caso de distribuições de dados com tendências não-lineares, que nós já abordamos no capítulo 1, quando falamos de Nearest Neighbour.
Para representarmos adequadamente uma distribuição de dados como a representada em (b) necessitamos de uma representação não-linear da distribuição, dada por uma curva principal da distribuição, como é mostrado na Figura abaixo.
Figura: Curva Principal

O cálculo exato de uma curva principal, porém, pode ser um processo matemático extremamente custoso, envolvendo interpolação polinomial ou outra técnica.
Quando discutimos Nearest Neighbour, no capítulo 1, e algoritmos que o utilizam, como IBL, no capítulo 2, vimos que existe a possibilidade de se aproximar um mapeamento de uma distribuição deste tipo através da divisão desta área curva em pedaços discretos, representados através de um conjunto de protótipos w0i. Isto está muito bem exemplificado pela facilidade com que IBL representa o problem ada espiral exatamente implementando esta técnica. Para gerarmos um conjunto de protótipos w0i deste tipo, porém, é necessário que a distribuição seja conhecida. Isto é fácil, quando temos, de antemão, associada a cada padrão, a sua categoria. Mas como proceder quando não conhecemos a distribuição dos dados nem quais classes existem ?
É aqui que a utilização de Redes de Kohonen se torna interessante: Helge Ritter demonstrou que uma rede de Kohonen aprende exatamente uma representação não linear discretizada deste tipo, sem necessidade de que se forneça de antemão as classes a que pertence cada padrão, realizando uma espécie de Análise Fatorial Não-Linear Discretizada. O resultado do processo de aprendizado, quando a convergência ocorreu adequadamente, é um mapeamento de subconjuntos da distribuição de dados a neurônios específicos da Rede A, que passam a fungir como protótipos para esses subconjuntos. Regiões vizinhas da distribuição são mapeadas para neurônios vizinhos no mapa de Kohonen A. O mecanismo de escolha do vencedor, similar a idéia do Nearest Neighbour, é o que garantre a não-linearidade da capacidade de representação da rede depois de treinada, agindo como uma função limiar, intrinsecamente não-linear, que determina as fronteiras entre cada subárea (subvolume) da distribuição mapeada. Isto pode ser visto na figura abaixo, onde uma classe é representada por um agrupamento (cluster) de neruônios em torno do vencedor S. O vencedor S representa com a maior aproximação o padrão X apresentado à rede..
Figura: Representação discretizada de uma distribuição não-linear de padrões aprendida por uma rede de Kohonen segundo Ritter.

Técnicas de Exploração de Dados Agrupados em Redes
Apropriedade estrutural das redes de Kohonen que vimos até agora coloca a pergunta: Não podemos de alguma forma aproveitar o fato de as redes de Kohonen estruturarem e organizarem topologicamente a informação aprendida ?
A resposta a essa pergunta é sim. Ao contrário das redes-BP, que necessariamente têm de ser encaradas como classificador de caixa-preta, as informações (e as abstrações) “aprendidas” por uma rede de Kohonen podem ser exploradas após o treinamento da rede e utilizadas das mais variadas formas.
Para finalizar este capítulo, vamos ver duas aplicações de redes de Kohonen.
A primeira delas se refere à utilização da informação contida em uma rede de Kohonen para guiar a busca de dados ainda desconhecidos que tenham a mais forte relação com um contexto atual de informação incompleta. Na verdade, trata-se da utilização de uma rede de Kohonen treinada como uma máquina de inferência neural que guia um processo de busca no sentido de se seguir pelo menor caminho na árvore de busca. Este trabalho foi realizado por nós no início da década de 1990 e apresenta uma solução para o problema de se explorar o espaço de possíveis soluções de maneira eficiente utilizando-se redes neurais.
A segunda é uma aplicação de treinamento de um braço-robô desenvolvida por Helge Ritter em 1989, onde se utiliza uma terceira camada de saída para uma rede de Kohonen, que controla um braço-robô de forma a que se mova para um ponto visualizado fornecido como dado de entrada. Esta não é propriamente uma aplicação de reconhecimento de padrões pura, mas mostra como extender uma rede de Kohonen através de uma camada de saída, aspecto pouco comentado na literatura.
Utilizando Mapas Auto-Organizantes como Máquinas de Inferência: KoDiag
No início da década de 1990 foi desenvolvido, pelo grupo de Sistemas Especialistas de Kaiserslautern, um sistema híbrido, denominado KoDiag [RW94, RW93, Wan93, RWW92, WR92], para diagnóstico baseado em casos utilizando uma Rede Neural de Kohonen modificada para dinamicamente atribuir pesos a atributos em função do contexto do problema e, assim, também realizar diagnóstico por meio do levantamento dirigido de atributos para o novo caso.
Para a implementação de KoDiag foi utilizado o princípio do mapeamento topológico da rede neuronal de Kohonen para o armazenamento de casos: casos mais similares são armazenados em áreas topologicamente próximas na rede. KoDiag utilizou pela primeira vez uma representação não simbólica para a base de casos, que era aprendida pela rede e ficava armazenada na mesma de forma sintética.
KoDiag utiliza a base de casos de PATDEX [Wes91, Wes93] para o treinamento da rede neural. Os casos são codificados como padrões especiais, e são representados de forma explícita: variáveis, valores de variáveis e diagnóstico. Dessa forma, o padrão de treinamento possui 3 partes: a primeira representa todas as variáveis do sistema; a segunda, todos os possíveis valores dessas variáveis; e a terceira, todos os diagnósticos. Dessa forma, um caso a ser treinado é representado com dois valores para cada variável: um para indicar a existência da mesma e outro para indicar seu valor.
Figura: KoDiag – no alto é mostrado o padrão de treinamento. No diagnóstico, somente a primeira parte era utilizada. Abaixo, o agrupamento ativo após apresentação do caso atual [RW94]
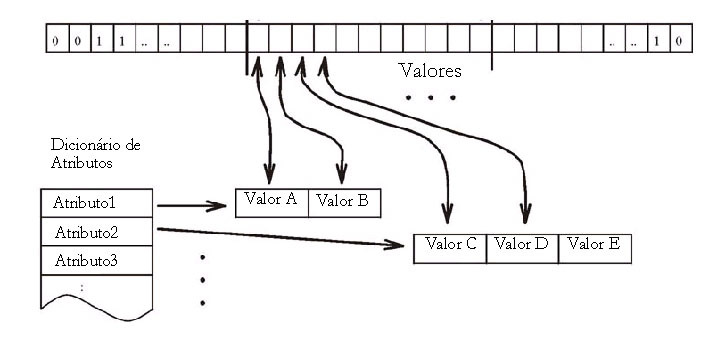
KoDiag podia realizar aquisição incremental dirigida de dados para diagnóstico com a apresentação de dados incompletos da situação atual. Caso a informação não bastasse para o diagnóstico, o agrupamento de neurônios ativado por esta apresentação era analisado e o valor da variável ainda desconhecida mais fortemente correlacionada a este agrupamento era solicitado para ser levantado pelo usuário. Um exemplo de um padrão em PATDEX pode ser visto abaixo:
Código Smalltalk descrevendo um caso de defeito em uma máquina CNC utilizado por KoDiag
PortableCase
newCase: #Toolarm10
withEnvironment: #(#(#IoStateIN32 #logical0) #(#Code #I41)
#(#ToolarmPosition #back) #(#IoStateOUT30 #logical0)
#(#IoStateOUT28 #logical1) #(#Valve21Y2 #switched)
#(#IoStateIN37 #logical1) )
describes: #IoCardFaultAtIN32i59
KoDiag é considerado um sistema de Raciocínio Baseado em Casos, em contraste com outros sistemas que também utilizam a codificação de casos em redes neurais, por utilizar uma interpretação autônoma passo a passo dos dados aprendidos na rede e guiar o usuário de forma inteligente no processo de levantamento de dados.
Qual é o objetivo de KoDiag ?
O ponto de partida para o desenvolvimento de KoDiag (Diagnóstico com Redes de Kohonen) foi a necessidade de se possibilitar o levantamento incremental de variáveis de um problema em uma situação de diagnóstico descrita como um padrão composto por pares atributo-valor: em muitas situações onde é necessário efetuar-se um diagnóstico de um problema não se possui de antemão valores para todas as variáveis do problema e tampouco todas as variáveis são necessárias para se determinar o diagnóstico correto para todas as situações.
Um exemplo é o domínimo de aplicação-exemplo de KoDiag: Diagnóstico de falhas em tornos de comando numérico:
- O estado de um torno CNC pode ser descrito por uma quantidade bastante grande de variáveis, como por exemplo a temperatura do óleo em diversas partes hidráulicas, o estado de diversos fusíveis, a mensagem de erro sinalizada no display de comando, o estado de desgaste da ferramenta de corte, etc.
- Quando um torno deixa de funcionar, dependendo do erro, apenas algumas dessas variáveeis terão relevância para se obter um diagnóstico correto da falha.
- Levantar o valor para todas é um processo desnecessário e custoso, uma vez que implica em tempo e, eventualmente, na necessidade de se desmonatr partes do torno ou de se realizar testes complexos para levantar o estado de uma peça ou parte mecânica.
- Partindo-se de um conjunto de variáveis iniciais, como por exemplo o código de erro mostrado pela máquina, é importante guiar o processo de levantamento de valores para as outras variáveis cujo valor ainda é desconhecido de maneira a otimizar o processo de busca de um diagnóstico. Para isso é preciso encontrar um caminho mínimo no espaço de pares variável-valor de maneira e levantar apenas os valores da variáveis relevantes ao contexto de falha atual e evitar levantar valores para variáveis desnecessárias, como por exemplo o estado do fusível da fonte de alimentação em uma situação onde o óleo de um componente hidráulico superaqueceu.
Esse procedimento é fácil de realizar em um sistema especialista para diagnóstico convencional baseado em regras ou em um sistema baseado em casos que utiliza uma matriz de relevância para conjuntos de pares variável-valor. Em muitas situações, porém, a relevância de variáveis para contexto é desconhecida e precisamos de uma técnica capaz de agrupar as informações de forma a representar esses contextos. A rede de Kohonen é ideal para isso pois possibilita a exploração da informação codificada na rede através da:
- apresentação incremental de padrões incompletos, que são considerados como o contexto atual ,
- da exploração da informação da rede, tomando-se os neurônios ativados por este contexto e seguindo-se os pesos de volta para a camada de entrada e vendo-se com qual valor ainda desconhecido este contexto correlaciona masi fortemente.
Como funciona KoDiag ?
KoDiag explora o fato de que uma rede de Kohonen mapeia valores de variáveis a contextos representados por grupos de neurônios na rede ativados por um padrão incompleto de forma a possibilitar o levantamento dirigido de novas informações.
A codificação de informação em KoDiag funciona da seguinte forma:
- Cada padrão é constituído de três partes: diagnóstico, variáveis, valores de variáveis.
- Para cada diagnóstico há um neurônio de entrada
- Para cada variável representando uma parte da máquina responsável por uma falha, há um neurônio de netrada.
- Para cada valor que essa variável pode assumir há também um neurônio de entrada. Para variáveis de domínios contínuos, discretiza-se o domínio em faixas de valores.
A rede é treinada com padrões que contém valor “1” para dois neurônios de entrada de cada variável que participa deste padrão: um valor para indicar a participação desta variável neste caso e outro para indicar qual valor que esta variável assumiu neste caso particular. Variáveis cujo valor é irrelevante para a situação são representadas por “0”. Dessa forma estamos associando a variável, indeopendentemente de seu valor à situação.O processo de diagnóstico, depois de treinada a rede, funciona então da seguinte maneira:
- É apresentado à rede um padrão incompleto inicial, contendo apenas os pares variável-valor capazes de serem levantados de forma fácil, por exemplo: a mensagem de erro emitida pela máquina e o fato de o óleo em um mancal estar superaquecido.
- Este contexto inicial é propagado pela rede e observa-se quais neurônios respondem a ele com uma ativação mínima. Este é o conjunto dos ActiveNeurons.
- Propagamos a ativação destes neurônios de volta para a parte dos diagnósticos da camada de entrada usando os pesos das conexões existentes. Se há um neurônio de diagnóstico que obteve ativação acima de um limiar mínimo e ao mesmo tempo diferente o suficiente dos outros, consideramos que o contexto foi suficiente para se chegar a um diagnóstico inequívoco e paramos.
- Se isto não acontece, propagamos a ativação dos ActiveNeurons de volta para a parte das variáveis da camada de entrada usando os pesos das conexões existentes. Buscamos o neurônio representando uma variável cujo valor ainda é desconhecido que tenha obtido a maior ativação. Este é um neurônio que durante o treinamento foi associado ao contexto atual de forma forte.
- Levantamos o valor da variável representada este neurônio, detalhando o nosso contexto. Este par atributo-valor é então apresentado isoladamente à rede.
- Determinamos o conjunto de nerurônios do mapa de Kohonen ativados por este par, que é denominado ChosenNeurons. Estes são os neurônios do mapa associados a este contexto atributo-valor independentemente dos outros valores que o acompanham.
- Realizamos a intersecção entre o conjunto anterior, ActiveNeurons e os ChosenNeurons, levando ao novo conjunto de ActiveNeurons, cujo tamanho é bastante menor. Este procedimento de redução progressiva do conjunto de neurônios do mapa considerados garante a convergência do processo.
- Novamente propagamos a ativação dos ActiveNeurons para a parte de diagnóstico da camada de entrada, retornando ao passo 3. O processo termina quando o teste do passo 3 for satisfeito ou os ActiveNeurons representarem um conjunto vazio.
Figura: Seleção de Neurônios

KoDiag foi testado com o mesmo conjunto de daods do sistema PATDEX, um sistem ade RBC estado-da-arte na época e os resultados obtidos foram bastante similares, tanto em termos de levantamento de variávesi quanto de resultados de classificação em função de perda de informação.
Utilizando Redes de Kohonen para a coordenação visumotora de um braço de Robô
Motivação: simulação das „cartas motoras“ encontradas em cérebros de mamíferos utilizando uma rede de Kohonen tridmensional com uma camada extra de saída representando os comandos de movimento do braço-robô.
Técnica: Modelar uma projeção F : V -> U de um espaço „sensorial“ V em um espaço de „comandos motores“ U.
a) criar uma projeção f dos „estímulos sensoriais“ V em uma carta tridimensional A
b) criar uma projeção da carta em um espaço de „comandos motores“ U.
Figura: Desenho da simulação utilizada por Helge Ritter

O modelo geral da projeção gerada pode ser visto na próxima figura. O objetivo é utilizar-se dois mapeamentos: um entre a camada de entrada e a de Kohonene outro entre camada de Kohonen e a de saída.
Figura: Mapeamento esperado
Algoritmo geral de treinamento:
- Registre a próxima ação de controle (v, u)
- Vencedor: calcule a posição na carta s := fw(v) que corresponde ao mapeamento do estímulo visual v na carta.
- Execute um passo de treinamento: IN
- Execute um passo de treinamento: OUT
- retorne a 1
Fórmulas: Passos de treinamento IN e OUT, respectivamente.
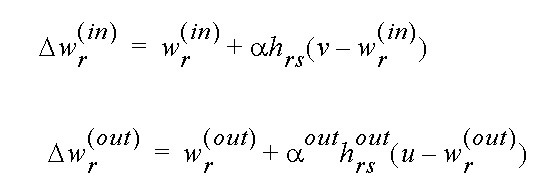
Estrutura da simulação para os movimentos do braço do robô:
- Posição do objeto dada por um vetor 4-dimensional
- Posição do braço do robô dada por um conjunto de 3 ângulos das juntas do braço.
Figura: Estrutura da simulação para os movimentos do braço do robô
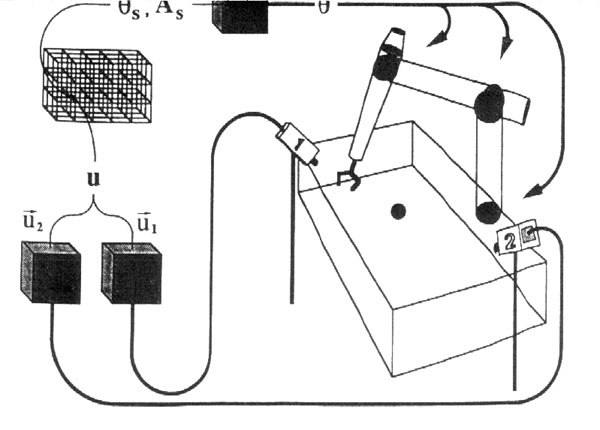
Resultados do treinamento podem ser vistos na próxima figura: com o passar do tempo a rede vai aprendendo a configuração tridimensional do espaço de movimentação do braço-robô e cada ponto do espaço na rede tridimensional é mapeado a um conjunto de ângulos das juntas do braço robô na camada de saída que movimenta o braço para aquela posição.
Figura: Treinamento
a) Espaços de Entrada e de Saída ao Início do Treinamento

b) Organizaçlão gradual da rede no espaço de saída durante o treinamento segundo Ritter
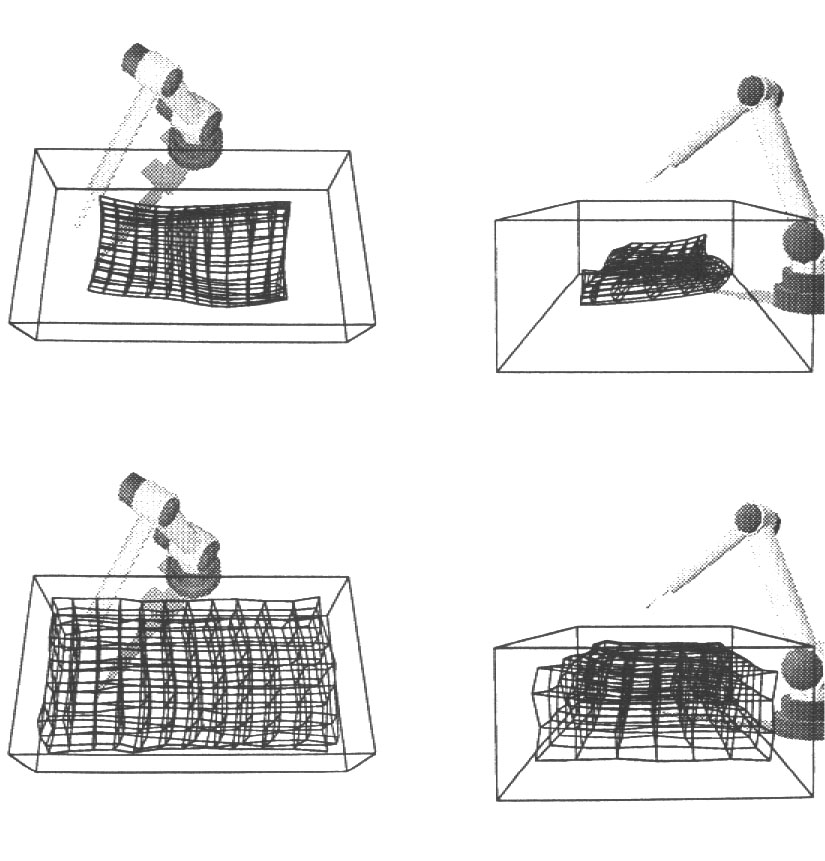
Referências
- [Koho88] Kohonen,Teuvo: Self-Organization and Associative Memory, Springer, 1988 (2. edition)
- [KR89] Kohonen,T., Ritter, H.; Self-Organizing Semantic Maps, Biol. Cybern., 61, 241-254, (1989)
- [RW93] J. Rahmel, A. von Wangenheim. The KoDiag System: Case-Based Diagnosis with Kohonen Networks. In Proceedings of the I International Workshop on Neural Networks Applications and Tools, Liverpool, IEEE Computer Society Press, 1993.
- [RW94] J. Rahmel, A. von Wangenheim. KoDiag: A Connectionist Expert System. In Proceedings of the IEEE International Symposium on Integrating Knowledge and Neural Heuristics, Pensacola, Florida, 1994.
- [RWW92] J. Rahmel, A. von Wangenheim, S. Wess. KODIAG: Fallbasierte Diagnose mit KOHONEN Netzen. In Proceedings of the GI Workshop Fälle in hybriden Systemen, Germany, 1992.
- [Wan93] A. von Wangenheim. Fallbasierte Klassifikation mit Kohonen Netzen. In Proceedings of the Workshop “Fälle in der Diagnostik”, XPS-93, Germany, Februar 1993.
- [Wes91] S. Wess. PATDEX/2: Ein fallbasiertes System zur technischen Diagnostik. SEKI-Working Paper SWP91/01, Department of Computer Science, University of Kaiserslautern, Germany, 1991.
- [Wes93] S. Wess. PATDEX – Inkrementelle und wissensbasierte Verbesserung von Aehnlichkeitsurteilen in der fallbasierten Diagnostik. In Proceedings of the 2. German Workshop on Expertsystems, Germany, 1993.
- [WR92] A. von Wangenheim, J. Rahmel. Fallklassifikation und Fehlerdiagnose mit Kohonen-Netzen. In Proceedings of the Workshop “Ähnlichkeit von Fällen”, Universität Kaiserslautern, Germany, 1992.
Exercício
Implemente você mesmo a estratégia de guia de diagnóstico do modelo KoDiag utilizando os dados de animais de Kohonen e Ritter, vistos na aula anterior, extendendo-os de forma a que contenham todo o set de dados: tando as características dos animais como a “classe” de cada vetor de características. Dessa forma você terá padrões de treinamento de no mínimo 23 entradas. Para tal, treine uma rede de Kohonen usando o SNNS de forma a que ela prenda as distribuições dos animais e gere o arquivo em “C” descrevendo esta rede. A seguir, utilize este código C e extenda-o permitindo que as ações de busca descritas acima sejam realizadas. Teste apresentando dados incompletos de animais e utilize a filosofia de guia de busca de KoDiag para decidir se você pode realizar o diagnóstico assim mesmo ou se você precisa levantar mais alguma característica e qual é esta característica que precisa ser levantada.
Páginas Correlatas neste Site
Reconhecimento de Padrões
Visão Computacional
- Deep Learning::Introdução ao Novo Coneccionismo
- Deep Learning::Reconhecimento de Imagens
- Deep Learning::Aprendizado por Transferência e Ajuste Fino
- Deep Learning::Segmentação Semântica
- Deep Learning::Redes Adversárias
- Deep Learning::Coisas Prontas & Datasets
- Deep Learning::Ensinando à Rede: Ferramentas de Anotação
- Deep Learning::Eu não gosto de escrever código! Ambientes de Programação Visual
Copyright © 2018 Aldo von Wangenheim/INCoD/Universidade Federal de Santa Catarina