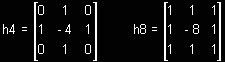O que é convolução ? Matematicamente, a convolução é uma operação entre duas matrizes, geralmente bidimensionais, uma das quais é a imagem e a outra é um matriz chamada de matriz de convolução ou elemento estruturante.
A matriz de convolução representa uma função matemática qualquer e é aplicada sobre cada pixel g(x,y) da imagem e sua vizinhança imediata, resultando em uma nova imagem gc(x,y), que reflete a relação da imagem original com a função matemática dada pela matriz.
Como realizamos a convolução ? Podemos considerar a convolução como a aplicação de uma máscara de resposta à imagem de acordo com critérios bem definidos. Na convolução temos dois componentes:
- Uma ou mais matrizes de convolução ci(x,y)
- A operação de convolução
A forma mais simples é quando temos apenas uma matriz de convolução e a operação de convolução é a soma dos resultados da multiplicação de cada elemento da matriz com a região da imagem sob a mesma e a subseqüente substituição do valor do pixel sobre o qual a matriz foi aplicada por este resultado.
Exemplo:
|
 |
- Observe que o resultado é sempre escrito na nova imagem resultante
- Observe que se o pixel sob a matriz se encontrar nas bordas da imagem, consideramos apenas os elementos sob a matriz.
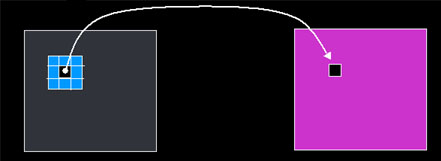
imagem original —> imagem resultante
E1.1 Detecção de pontos salientes
A aplicação de convolução mais simples é a detecção de pontos salientes na imagem. Um ponto saliente é um ponto cujo valor se destaca de seus vizinhos, não necessariamente um valor alto do ponto de vista absoluto.
E1.2 Convolução Genérica
A aplicação de convolução simples pode ser extendida para outros tipos de matriz de filtragem que podem suavizar ou modificar a imagem. É importante possuir-se um programa que leia uma matriz qualquer e aplique o método utilizando:
- Qualquer matriz quadrada de convolução ci(x,y) de dimensões ímpares
- A operação de convolução é sempre a soma das multiplicações das posições correspondentes sob a matriz.
- O pixel de aplicação R é sempre o valor sob o elemento central da matriz
O operador de Laplace é utilizado para a detecção de cruzamentos por zero da Segunda Derivada em uma imagem e não possui direção específica, ao contrário do que veremos nos detectores de bordas de Sobel, Roberts, Robinson e outros, adiante.
Há duas variantes, uma utilizada para consideração de vizinhanças-de-4, h4, e outra para levar em consideração vizinhanças-de-8, h8.
Requisitos para E1.1, E1.2 e E1.3
- Duas entradas: imagem e matriz de convolução
- Ler as duas entradas tanto em P2 como em P5
- Uma saída: Imagem resultante.
possui graduação em Ciências da Computação pela Universidade Federal de Santa Catarina (1989) e Doutorado Acadêmico (Dr. rer.nat.) em Ciências da Computação pela Universidade de Kaiserslautern (1996). Atualmente é professor Titular da Universidade Federal de Santa Catarina, onde é professor do Programa de Pós-graduação em Ciência da Computação e dos cursos de graduação em Ciências da Computação e Sistemas de Informação. Tem experiência nas áreas de Informática em Saúde, Processamento e Análise de Imagens e Engenharia Biomédica, com ênfase em Telemedicina, Telerradiologia, Sistemas de Auxílio ao Diagnóstico por Imagem e Processamento de Imagens Médicas, com foco nos seguintes temas: analise inteligente de imagens, DICOM, CBIR, informática médica, visão computacional e PACS. Coordena o Instituto Nacional de Ciência e Tecnologia para Convergência Digital - INCoD. Foi o criador e primeiro Coordenador do Núcleo de Telessaúde de Santa Catarina no âmbito do Programa Telessaúde Brasil do Ministério da Saúde e da OPAS - Organização Pan-Americana de Saúde e criador do Núcleo Santa Catarina da RUTE - Rede Universitária de Telemedicina.