
- :: Home
- :: Downloads
- :: Contacts
- :: What's news
SMS - The supervised color image segmentation method
Image segmentation is one of the most important tools in computer vision and
image understanding. Its use can be extended to different application areas,
such as medical imaging, robot navigation, aerospace industry, security control
and many others. Among the most popular image segmentation concepts are the
variational models, more specifically the Mumford-Shah model [MumfordShah89]. This model
uses low-level vision to segment a domain of an image I into segments. The basic
idea is merging the regions on which the signal I is homogeneous and is
delimited by a system of regular discontinuities K, in order to make visible the
objects on the scene.
In this work a novel region-merging image segmentation approach is presented.
This approach is based on a two-step procedure: a distance metric is learned
from some features on the image, then a piecewise approximation function for the
Mumford-Shah model is optimized by this metric. The global optimum of the
approximation function is inductively achieved under high polynomial terms of
the Mahalanobis distance [Grudic06], extracting the nonlinear features of the
pattern distributions into topological maps. The penalizer terms of the
Mumford-Shah equation are based on new similarity criteria, computed from the
topological maps and the class label information.
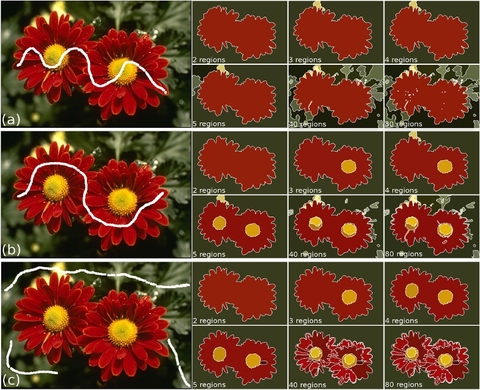
Figure 1 - merging evolution #1

Figure 2 - merging evolution #2
Besides providing the image results obtained with our method, we aim to
objectively compare its quality with other state-of-art algorithms. For this
goal, we have selected four distance measures developed for image segmentation
evaluation. These measures -- Rand [Rand71], Fowlkes-Mallows [Fowlkes83], Jacard
[Jacard02] and Dongen [Dongen00] -- result in float values are in the [0,1] interval,
where the closest to 0 the better the segmentation is.
All these evaluation techniques are ground-truth based evaluation methods. So,
every image set selected has to have a group of ground-truth images available
for the evaluation of the experiments. For this reason, we selected our test
sets from the Berkeley Segmentation Dataset and Benchmark
For this purpose, we selected 60 images from the Berkeley Image Dataset, where the following experiments were performed:
1- A merging evolution experiment in order to verify the influence of this approximation function to the Mumford-Shah model;
2- A direct comparison against the conventional Mumford-Shah model using the vector norm as discrimination function;
3- A comparison among different image segmentation approaches using the aforementioned evaluation indexes. In this experiment we used the methods:
* (S-MS) - The proposed supervised image segmentation approach (Computer Vision and Image Understanding - 2011).
* (MS) - The conventional Mumford-Shah Model [Megawave10].
* (CSC) - Color Structure Code [RehrmannPriese98].
* (EDISON) - the edge detection and image segmentation system [ComaniciuMeer02].
* (WS) - the classical Watershed algorithm [VincentSoille91].
* (JSEG) - the unsupervised color image segmentation method [DengManjunath01].
* (RHSEG) - a hierarquical image segmentation [Tilton06].
* (GNM and GNM2) - two versions of a Gradient Network Method previously published. This method is a post-processing segmentation, which can be combined with other methods. [Wangenheim09].
The results we obtained show a better discrimination of object boundaries and
the location of regions when compared against the conventional Mumford-Shah and the state-of-the-art algorithms, as presented in our results page.
You also can download the evaluation tables, objective evaluation sources and the segmentation results we obtained.
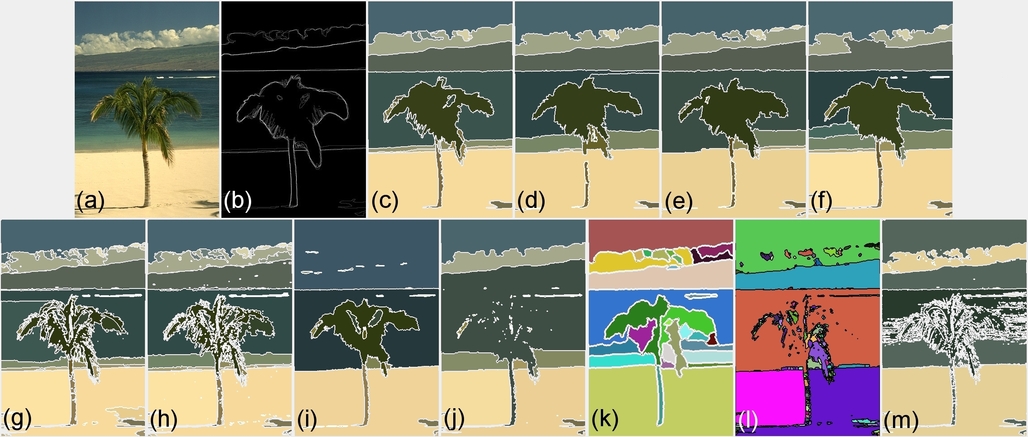
Figure 3 - Comparison among other image segmentation methods: (a) original image, (b) ground-truth, (c) S-MS, (d) MS+gnm2, (e) CSC+gnm2,
(f) MS, (g) MS+gnm, (h) CSC+gnm,
(i) Edison, (j) CSC, (k) JSEG, (l) WS and in (m) RHSEG
References
[MumfordShah89] D. Mumford, J. Shah, Optimal approximations by piecewise smooth
functions and associated variational
problems, Commun. Pure Appl. Math. 42 (1989) 577-684.
[Grudic06] G. Grudic. J. Mulligan, Outdoor path labeling using polynomial
Mahalanobis distance, Robotics: Sci-
ence and Systems II Conference. 2006.
[Rand71] W. M. Rand, Objective criteria for the evaluation of clustering methods,
Journal of American Statistical
Association 66 (1971) 846-850.
[Fowlkes83] E. B. Fowlkes, C. L. Mallows, A method for comparing two hierarchical
clusterings, Journal of the
American Statistical Association 78 (383) (1983) 553-569. URL
http://www.jstor.org/stable/2288117
[Jacard02] A. Ben-Hur, A. Elissee, I. Guyon, A stability based method for
discovering structure in clustered data,
in: Pacific Symposium on Biocomputing, 2002, pp. 6-17.
[Dongen00] S. Dongen, Performance criteria for graph clustering and markov cluster
experiments, Tech. rep., Am-
sterdam, The Netherlands, The Netherlands (2000).
[Martin01] Martin, D., Fowlkes, C., Tal, D., Malik, J. A database of human
segmented natural images and its application to evaluating segmentation
algorithms and measuring ecological statistics. In: Proc. 8th Int'l Conf.
Computer Vision. vol. 2; 2001. p. 416-423.
[Rehrmann98] Rehrmann, V. and Priese, L. Fast and Robust Segmentation of Natural Color Scenes. ACCV (1), 1998: 598-606.
[Wangenheim09] Wangenheim, A. V., Bertoldi, R. F., Abdala, D. D., Sobieranski, A., Coser, L., Jiang, X., Richter, M. M., Priese, L., and Schmitt, F. 2009. Color image segmentation using an enhanced Gradient Network Method. Pattern Recogn. Lett. 30, 15 (Nov. 2009), 1404-1412. DOI= http://dx.doi.org/10.1016/j.patrec.2009.07.005
[Megawave10] http://megawave.cmla.ens-cachan.fr/. Access in: 17 may 2010.
[ComaniciuMeer02] D. Comaniciu, P. Meer. Mean Shift: A Robust Approach Toward Feature Space Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence; 2002; 24 (5); 603-619.
[VincentSoille91] L. Vincent and P. Soille. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. In Transactions on Pattern Analysis and Machine Inteligence, volume 9, pages 735-744. IEEE, 1991.
[DengManjunath01] Deng, Y., Manjunath B.S. Unsupervised segmentation of color-texture regions in images and video. IEEE Transactions on Pattern Analysis and Machine Intelligence; 2001; 23(8):800-810.
[Tilton06] Tilton, J.C. D-dimensional formulation and implementation of recursive hierarchical segmentation, Disclosure of Invention and New Technology: NASA Case No. GSC 15199-1, May 26, 2006.