Métodos no Domíno do Espaço 2: Detecção de Bordas

Introdução

Borda é o contorno entre um objeto e o fundo indicando o limite entre objetos sobrepostos Um CONTORNO é uma linha fechada formada pelas bordas de um objeto. Mas como conceituamos e detectamos uma borda computacionalmente?

Variações de intensidade complexas que ocorrem em uma região são geralmente chamadas de textura. Bordas são definidas como picos da magnitude do gradiente, ou seja, são variações abruptas que ocorrem ao longo de curvas baseadas nos valores do gradiente da imagem. As bordas são regiões da imagem onde ocorre uma mudança de intensidade em um certo intervalo do espaço, em uma certa direção. Isto corresponde a regiões de alta derivada espacial, que contém alta frequência espacial. 

• Borda unidimensional : pode ser definida como uma mudança de uma intensidade baixa para alta. A intensidade do sinal pode ser interferida por ruídos.

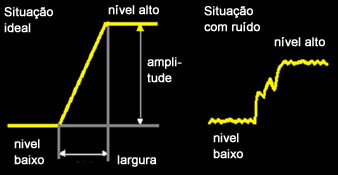Gráfico da intensidade de uma imagem

• Borda bidimensional: as descontinuidades ocorrem ao longo de certas linhas ou orientações A orientação é uma característica importante em bordas 2-D 

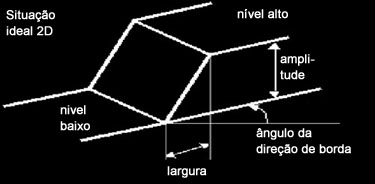Gráfico da intensidade representando uma borda bidimensional.

A aquisição da imagem está sujeita a algum tipo de ruído, a situação ideal (sem ruído), na prática não existe. Ruídos não podem ser previstos pois são de natureza randômica e não podem nem mesmo ser medidos precisamente. Porém, algumas vezes ele pode ser caracterizado pelo efeito na imagem, e é geralmente expresso como uma distribuição de probabilidade com uma média específica e um desvio padrão. Existem dois tipos de ruídos específicos: 

• Ruído independente do sinal: é um conjunto randômico de níveis de cinza, estatisticamente independente dos dados da imagem. Este tipo de ruído acontece quando a imagem é transmitida eletronicamente de um lugar para outro. 
  • A – imagem perfeita 
  • N – é o ruído 
  • B – imagem final 
  • B= A+N 

• Ruído dependente de sinal: o nível do valor de ruído a cada ponto na imagem é uma função do tom de cinza.
  

Operadores para detecção de bordas – Operadores de derivadas

Uma vez que uma borda é definida por uma mudança no tom de cinza, quando ocorre uma denscontinuidade na intensidade, ou quando o grandiente da imagem tem uma variação abrupta, um operador que é sensível a estas mudanças operará como um detector de bordas.

Um operador de derivada faz exatamente esta função. Uma interpretação de uma derivada seria a taxa de mudança de uma função, e a taxa de mudança dos níveis de cinza em uma imagem é maior perto das bordas e menor em áreas constantes. Se pegarmos os valores da intensidade da imagem e acharmos os pontos onde a derivada é um ponto de máximo, nós teremos marcado suas bordas. Dado que as imagens são em duas dimensões, é importante considerar mudanças nos níveis de cinza em muitas direções. Por esta razão, derivadas parciais das imagens são usadas, com as respectivas direções X e Y. Uma estimativa da direção atual da borda pode ser obtida usando as derivadas x e y como os componentes da direção ao longo dos eixos, e computar o vetor soma. O operador envolvido é o gradiente, e se a imagem é vista como uma função de duas variáveis A(x,y) então o gradiente é definido como: 

Grupo E3 – Detecção de Bordas com Convolução Simples

E3.1 Roberts

É o mais antigo e simples algoritmos de detecção de bordas. Publicado em L. Roberts Machine Perception of 3-D Solids, Optical and Electro-optical Information Processing, MIT Press 1965. Utiliza uma matriz 2×2 para encontrar as mudanças nas direções x e y. 

Máscara ou Kernel de Convolução de Roberts: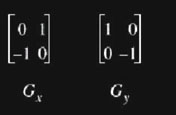 

Para determinar onde o pixel avaliado é ou não um pixel de borda, o gradiente é calculado da seguinte forma: 

Fórmula para cálculo do gradiente: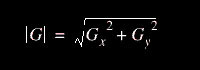 

Se a magnitude calculada é maior do que o menor valor de entrada (definido de acordo com a natureza e qualidade da imagem que esta sendo processada), o pixel é considerado ser parte de um borda. A direção do gradiente da borda, perpendicular a direção da borda, é encontrada com a seguinte fórmula:

Fórmula para cálculo da magnitude: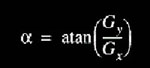 

O pequeno tamanho da máscara para o operador de Roberts torna o mesmo fácil de se implementar e rápido para calcular a máscara de resposta. As
respostas são muito sensíveis ao ruído na imagem.

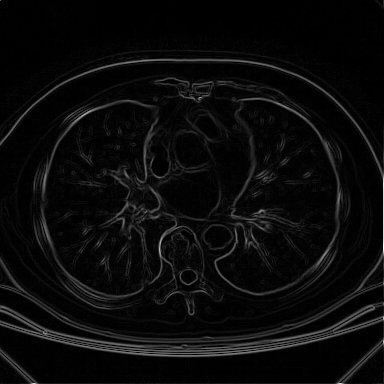
Resultado da aplicação da implementação do Khoros do operador de Roberts
sobre a imagem de tomografia mostrada anteriormente.

E3.2 Sobel

Utiliza duas máscaras para encontrar os gradientes vertical e horizontal das bordas.
Máscaras de Sobel: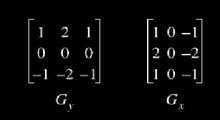 
Considerações sobre o operador de Sobel

• A fórmula para encontrar o gradiente e o ângulo são as similares ao operador de Roberts. 
• A computação de |G| se torna mais complexa. Na prática |G| é aproximada da seguinte forma: |G|= |Gx| + |Gy|. 
  • O ângulo do gradiente corresponde direção de máxima variação da intensidade 
• Devido as máscaras serem 3X3 ao invés de 2X2, Sobel é muito menos sensível ao ruído do que Roberts. 
• Os resultados são mais precisos e o módulo do gradiente é proporcional a derivada local da intensidade. 

Extensões ao método de Sobel

1. Alguns autores incluem uma terceira matriz para encontra gradientes diagonais, mostrada abaixo. Netse caso temos três e não duas matrizes para o cálculo dos gradientes. 
2. Alguns autores trabalham com mais três matrizes, que são as negações das três vistas até o momento. Isto permite que se identifique não só a direção mas também o sentido do crescimento do gradiente. Pode ser útil.

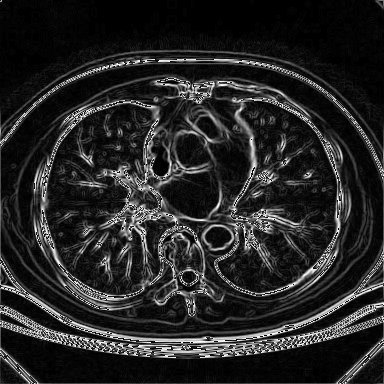
Resultado da aplicação da implementação do Khoros do operador de Sobel 
sobre a imagem de tomografia mostrada anteriormente.

E3.3 Robinson

É similar em operação ao de Sobel, porém usa um conjunto de oito máscaras, onde quatro delas são as seguintes: 

As outras quatro são simplesmente negações destas quatro.

A magnitude do gradiente é o valor máximo obtido ao aplicar todas as oito máscaras ao pixel vizinho, e o ângulo do gradiente pode ser aproximado como o ângulo na linha de zeros na máscara dando a resposta máxima. Abaixo as quatro matrizes acima com seus respectivos ângulos de preferência:

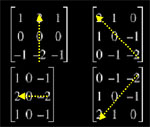
As matrizes negadas possuem mesma direção, mas sentido oposto como ângulo preferencial. 
Este algoritmo aumenta a precisão de |G|, mas requer mais computação do que as versões tradicionais de Roberts e Sobel, devido à quantidade de máscaras.

E3.4 Prewitt

O operador de Prewitt é muito similar à versão de 6 matrizes do Operador de Sobel. O que varia é apenas o conjunto de valores das matrizes de convolução, que são definidas como segue:

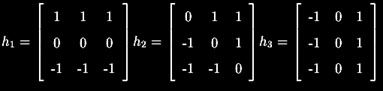
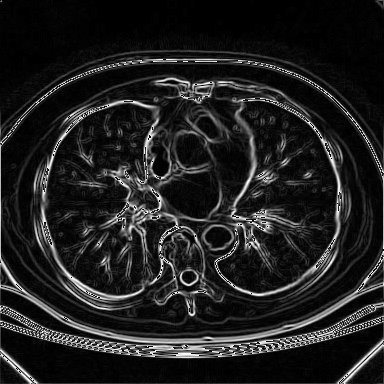
Resultado da aplicação da implementação do Khoros do operador de Prewitt 
sobre a imagem de tomografia mostrada anteriormente.

E3.5 Isotrópico

Um operador isotrópico em análise de imagens é um operador que responde de forma igual a variações de intensidade em toda e qualquer direção em uma imagem, sem qualquer preferência por uma direção ou conjunto de direções específico. Um exemplo típico é o detector de cruzamento por zero que responde de forma igual a bordas (na verdade a gradientes) em quaisquer direções. A utilização de suavização gaussiana também atua dessa forma. Na pratica costuma-se utilizar cruzamentos por zero associados a uma suavização gaussiana prévia da imagem. O operador para encontrar cruzamento spor zer pode ser o Laplaciano descrito anteriormente. 

No exemplo abaixo não sabemos qual matriz de convolução foi utilizada pois a documenttação do Khoros não menciona e não tentamos fazer negenharia reversa no código-fonte para descobrir. Fica apenas como exemplo. Este operador não vamos implementar. 

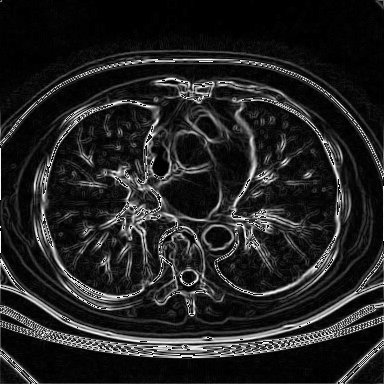
Resultado da aplicação da implementação do Khoros do operador  isotrópico 
sobre a imagem de tomografia mostrada anteriormente.