The research on Color Image Segmentation that has been performed in the particular field of Region-Growing Segmentation algorithms has been centered on different aspects of image segmentation strategies: representation of global criteria for region merging (e.g. the Gradient Network Method – http://www.lapix.ufsc.br/gnm/), cue identification or integration of texture information into the segmentation process. In order to overcome limitations imposed by the traditional linear colorspaces such as RGB, which do not represent adequately the perceptual differences of image ares in a given context, differente approaches have benn followed: different evaluation methods for chromacity and luminosity have been used ([Dony and Wesolkowski, 1999] and [Schneider et al., 2000]) and also approaches where the segmentation switche sto differente colorspaces to differentiate regions of clear and rough color perception in the scene of the image, as originally discussed by [Huang et al., 2006].
We played with the idea that, instead of defining complex, multi-step model-based schemes for color evaluation in images, why not define a particular colorspace that reflects the color distribution encontred in the images of a specific application area and use it for the measure of color distances in traditional region-growing segmentation algorithms ?
This site was created to present results achieved with traditional, well-accepted Region-Growing segmentation algorithms, when an Adapted Color Space is used instead of a simple linear colorspace. This adapted colorspace should be a colorspace defined by the color distribution encontered in the image itself. The first empirical evaluations that we have performed were achieved using the Mumford and Shah segmentation algorithm [Mumford and Shah, 1989], which is well-known and has an extremely simple structure, in combination with the Mahalanobis Distance, which defines a statistically inspired data-driven non-isotropic distance measure [Mahalanobis P.C. 1936].
We also show a generalization test where images of the same context are used. This experiment can be viewed here
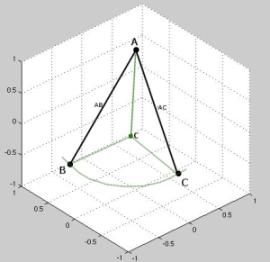 |
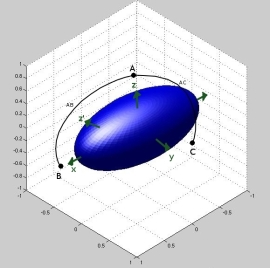 |
| Fig. a: A linear colorspace | Fig.b: A non-isotropic Colorspace |
For the validation of the results obtained so far, we have selected two segmentation quality measures developed especially for image segmentation evaluation. These measures, the Rand Index [Rand71] and the Bipartite Graph Matching Method [Cheng et. al.01], provide results in float values which are in the [0,1] interval. These methods are based on two different quality assessment assumptions that we consider to be representative for the state of the art in research on automated image segmentation validation.
Both Rand and BGM are ground-truth based evaluation measures. So, every image set selected has to have a reliable group of ground-truth images available for the evaluation of the experiments. For this reason, we selected our test sets from the Berkeley Segmentation Dataset and Benchmark [Martin et.al.01], a well-known natural images dataset that has at least 5 and up to 7 ground-truths for every image in its dataset. The results of evaluation measures can be downloaded here.
REFERENCES
[Cheng et. al.01] H.D. Cheng, X.H. Jiang, Y. Sun and J. Wang. Color image segmentation: advances and prospects. Pattern Recognition 34, 2001, pp. 2259-2281.
[Dony&Wesolkowski99] Dony, R.D., Wesolkowski, S.B. 1999. Edge detection on color images using RGB vector angles. In: Proc. 1999 IEEE Canadian Conf. Electrical and Computer Engineering. Edmonton, Alberta, Canada May 9–12, pp. 687–692.
[Martin et.al.01] Martin, D., Fowlkes, C., Tal, D., Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proc. 8th Int’l Conf. Computer Vision. vol. 2; 2001. p. 416-423.
[Mahalanobis P.C. 1936], On the generalized distance in statistics, Proceedings of the National Institute of Science of India 12, 49-55. 1936.
[Mumford and Shah, 1989] D. Mumford and J. Shah, Optimal approximations by piecewise smooth functions and associated variational problems, Commun. Pure Appl. Math. 42, pp. 577–684. 1989.
[Rand71] W. M. Rand. Objective criteria for the evaluation of clustering methods. Journal of the American Statistical Association. Vol. 66. pp 846/850, 1971.
[Schneider et al., 2000] M.K. Schneider, P.W. Fieguth, W.C. Karl and A.S. Willsky, Multiscale methods for the segmentation and reconstruction of signals and images, IEEE Trans. Image Process. 9 (3) 2000, pp. 456–468 March. Full Text via CrossRef | View Record in Scopus | Cited By in Scopus (18)