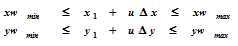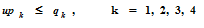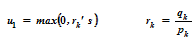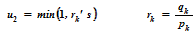Contents
- 1 Métodos para Cálculo de Visualização em 2D
- 2 O Sistema de Coordenadas Normalizado
- 3 Alternativas ao Sistema de Coordenadas Normalizado
- 4 Como eu navego no Mundo usando o CPP ?
- 5 Como uso o CPP na prática ?
- 6 SCN ou CPP?
- 7 O que é clipping?
- 8 Recorte de Pontos
- 9 Recorte de Linhas
- 10 Recorte de Linhas usando representação paramétrica da reta
- 11 Recorte de Linhas de Cohen-Sutherland:
- 12 Recorte de linhas de Liang-Barsky
- 13 Recorte de linhas de Nicholl-Lee-Nicholl
- 14 Clip windows não retangulares
- 15 Recorte de windows na forma de polígonos côncavos:
- 16 Recorte de polígonos
- 17 Outros tipos de Recorte
- 18 Exercício 1.3: Implementando Clipping
Coordenadas de Window e Clipping
Neste capítulo vamos abordar duas coisas muito importantes: um sistema de coordenadas que vai nos permitir um grau de liberdade muito maior na navegação com a window pelo mundo e uma técnica de otimização de visualização que nos permitirá determinar quais partes do mundo serão mostradas na tela e assim calcular apenas a visualização destas, chamados Métodos de Clipping ou de Recorte. Além disso veremos conceitos como: View Up Vector, Sistema de Coordenadas Normalizado ou de Window.
Métodos para Cálculo de Visualização em 2D
Para motivar este capítulo vamos recapitular alguns dos conceitos mais importantes vistos até o momento: para representar um mundo virtual qualquer em uma tela de computador, precisamos, além de uma estrutura de dados denominada display file, que contém esse mundo, de três outras entidades. Estas entidades são: uma área virtual, que representa uma parte do mundo qu queremos mostrar, uma área física, que representa uma parte do vídeo onde queremos desenhar esta parte do mundo e uma transformação que nos permite calcular como vamos desenhar esta parte do mundo no vídeo. Chamamos a estas entidades de:
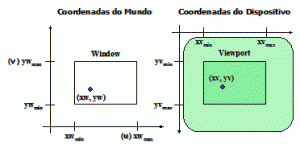 |
- Window (estrutura de dados – janela): Uma área de world-coordinates (coordenadas do mundo) selecionada para ser mostrada;
- Viewport (estrutura de dados – área de desenho da tela): Uma área em um dispositivo de display para a qual o conteúdo de uma window é mapeado;
- Transformação de visualização (transformação – viewing transform): É o mapeamento de uma parte de uma cena em coordendas do mundo para coordenadas de dispositivo. Executado pela transformada de viewport.
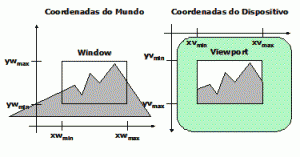 |
Até o momento vimos apenas uma forma de realizar a transformação de visualização. Esta forma é através de um mapeamento direto da window para a viewport.
Desvantagens do mapeamento direto window => viewport
- Navegação limitada;
- Eixos de coordenadas de window e de viewport são sempre paralelos;
- Transformada de viewport é apenas um transformação de escala;
- Operações como rotação da window são impossíveis.
Para adquirir independência de dispositivo, os windows são tipicamente definidos dentro de um quadrado unitário ou normalizado (normalized coordinates)
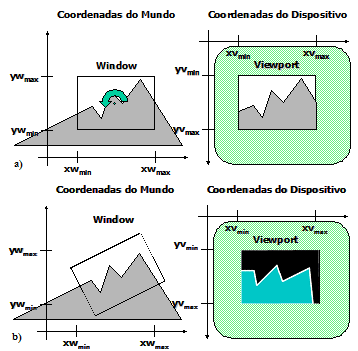
Estendendo o conceito de Window
Window: Para permitir todos os graus de liberdade na navegação no mundo, uma window deveria ser um retângulo com qualquer orientação. Até agora foi visto apenas windows paralelas ao sistema de coordenadas do mundo. Para extendermos uma window de forma a podermos realizar o efeito de panning, mesmo em 2D, temos de definir um terceiro sistema de coordenadas intermediário, entre o sistema de coordenadas do mundo e o sistema de coordenadas do vídeo. Este sistema de coordenadas pode ser chamado de sistema de coordendas normalizado ou sistema de coordenadas de plano de projeção.
 |
O Sistema de Coordenadas Normalizado
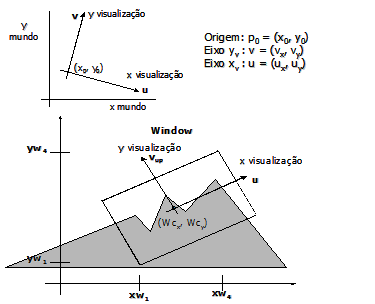
Para criar um esquema flexível de referência para a especificação do window em relação às coordenadas do mundo criou-se o sistema de coordenadas normalizado – SCN. Este sistema de coordenadas definia um conjunto de coordenadas próprias para a window. Era chamado de normalizado porque se definia a window como tendo tamanho unitário quando representada nele.
O SCN é um nível de representação intermediário entre as coordenadas de tela (viewport) e as coordenadas de mundo (WC). Como define um novo sistema de coordenadas próprio para a window, permite um grau de liberdade a mais na navegação com a window: a rotação da window. Calcular a visualização do mundo agora tem de ser realizado em duas etapas: a) Mapear do mundo para o SCN e b) mapear do SCN para coordenadas de viewport. O mapeamento SCN => viewport é uma transformação de escala apenas, pois seus eixos de coordenadas são paralelos para windows retangulares.
 |
Para uma determinada viewport conhecida, podemos calcular uma única matriz de transformação composta em coordenadas homogêneas. Toda vez que movemos ou rotacionamos a window temos de recalcular esta matriz de transformação. Fazer isto, porém, tem implicações sobre o cálculo do que é visível e do que cai fora da window/viewport. Veremos isto mais adiante. O procedimento padrão, se desejamos utilizar SCN, é mapear de WC para SCN e guardar estas coordenadas.
Implicações do sistema de coordenadas normalizado
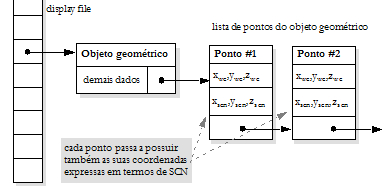
Cada objeto do mundo agora é representado em dois sistemas de coordenadas:
- Coordenadas do Mundo: suas coordenadas reais. Abreviamos por WC – World Coordinates;
- Coordenadas Normalizadas: coordenadas do objeto expressas em termos de u e v, com origem em (Wcx, Wcy). Estas coordenadas são recalculadas toda vez que movemos, escalonamos ou rotacionamos a window. Tradicionalmente normalizadas dentro da window para o intervalo [0,1] ou [-1,1]. No exemplo da figura acima estamos utilizando [-1,1] pois colocamos a origem no centro da window. Para usar [0,1] teríamos de colocar a origem no canto inferior esquerdo da window.
O display file pode se extendido para suportar esta representação intermediária, se o desejarmos, da forma como está descrito abaixo..
 |
Por que o nome sistema de coordenadas normalizado ?
Antigamente, para tornar um sistema independente do tamanho da viewport e facilitar alguns algoritmos, tornando-os genéricos, usava-se normalizar as coordenadas dos objetos:
- Fixava-se os extremos da window em (-1,-1),(1,1) ou (0,0),(1,1);
- Ao se transformar de um sistema de coordenadas para o outro, normalizava-se os objetos:
- Vantagem: tudo que possuir uma coordenada fora do intervalo escolhido está fora da window;
- Desvantagem: qualquer operação de navegação ou zoom implica em uma nova transformação de normalização de coordenadas, bastante custosa quando não se dispõe de hardware acelerador gráfico com capacidade de multiplicação matricial.

Alternativas ao Sistema de Coordenadas Normalizado
Pode-se continuar a representar a window em termos das unidades de medida do sistema de coordenadas do mundo, apenas introduzindo um novo sistema de eixos de coordenadas sempre paralelos às bordas da window. Chamamos este sistema de sistema de coordenadas de plano de projeção – CPP.
Quando não possuímos um hardware gráfico com capacidades de processamento de matrizes à nossa disposição e temos de realizar todas as operações via software, o uso do CPP possui várias vantagens:
- Mantem a unidade de medida do mundo: muito menos operações de divisão;
- Representa Vup por (xw1, yw1)(xw2, yw2) ao invés de (Wcx, Wcy)(vupx, vupy)
Uma vez representados os objetos do mundo em CPP, para todas as operações de navegação que utilizem apenas translações, podemos representar cada operação diretamente no CPP, sem necessidade de recálculo do mapeamento WC => CPP, apenas através de somas e subtrações, sem necessidade de operações matriciais.
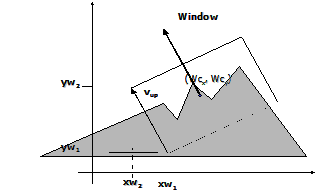 |
Criando uma representação de um mundo em CPP: Transformamos o sistema de coordenadas para um sistema com origem em Wc e eixos paralelos aos limites da Window. O processo é extremamente simples:
- Se vup for paralelo ao eixo Y, apenas transladamos Wc para a origem e aplicamos a transformada de viewport;
- Se vup não for paralelo ao eixo Y, rotacionamos o mundo e a window em torno de (Wcx, Wcy) por -§(Y, Vup);.

 |
Como representar e usar o CPP ?
Para representar e usar o CPP, altere o display file. Cada objeto gráfico de seu display file passará a possuir dois conjuntos de coordenadas:
Altere a definição da Window: será representada por dois conjuntos de coordenadas também: WC e CPP. Isto é diferente do SCN. Ali não precisávamos representar a própria window em SCN.
Utilize a representação em CPP dos objetos e da window para a transformada de Viewport.
O referencial do usuário que está sentado ao computador é o CPP
 |
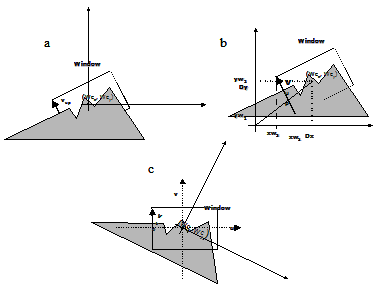
Como implementar a translação da window quando estiver em uma orientação não paralela aos eixos?
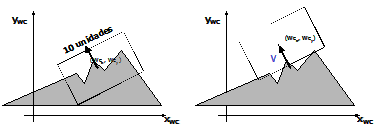
Considere o desenho anterior e idealize um “sistema de navegação 2D” para seu ambiente gráfico. Este sistema de navegação é bastante simples: ele possui 4 botões de “deslocamento” da window, que movem a window para “cima”, para “baixo”, para a “esquerda” e para a “direita” no sistema de CPP, que é o sistema de coordenadas no qual a tela de computador do usuário “viaja”. A movimentação da window “para cima” ficaria assim:
 |
Como uso o CPP na prática ?
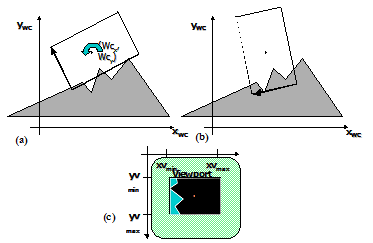
A utilização do sistema de Coordenadas do Plano de Projeção como sistema de coordenadas para a window nos traz uma série de vantagens em relação ao SCN – Sistema de Coordenadas Normalizado, pois não é necessário retransformar todo o mundo para o CPP a cada operação de navegação com a window, como teria de ser feito no SCN. No CPP a window não se encontra necessariamente na origem do sistema de coordenadas, mas sim navega livremente nele. A única exigência do CPP é que seus eixos sejam paralelos às bordas da window para que os algoritmos de clipagem que vamos ver adiante possam funcionar de forma eficiente. No CPP apenas relizamos uma transformação de sistema de coordenadas e recalculamos a representação do mundo em CPP quando a window sofreu uma operação de rotação durante a navegação pelo mundo, como mostrado na See Rotação da window durante a navegação peloi mundo 2D. Estamos com a window como mostra (a) e desejamos modificar a direção de “caminhada” da window, rotacionando-a em 85 graus no sentido anti-horário. Para tanto a window roda em torno de seu centro e termina na posição mostrada em (b). acima. Em todos os outros casos de navegação ou de zoom a window simplesmente é transladada no CPP, o que torna o processo bem mais eficiente.
Para usar o CPP, podemos estender o display file de uma forma bastante simples. Basta-nos estender cada estrutura de dados que representa algum objeto geométrico de forma a possuir duas representações: uma no sistema de coordenadas do mundo e outra do CPP. Toda vez que uma operação de rotação na window fizer com que tenhamos que rotacionar o sistema de referência do CPP, recalculamos os valores das coordenadas de CPP de cada objeto do display file com base nas coordenadas de mundo deles.
 |
SCN ou CPP?
Vimos duas formas de se realizar a representação intermediária entre o sistema de coordenadas do mundo e a viewport: o SCN e o CPP. Uma delas você vai precisar se desejar que seu SGI seja capaz de oferecer ao usuário a possibilidade de rotacionar a window ao navegar no mundo 2D e, mais tarde, quando virmos 3D, você não vai encontrar nenhum caminho para realizar a navegação que não passe por uma representação intermediária desse tipo.
A pergunta, porém é: qual representação é mais vantajosa ? Resumimos abaixo as vantagens e desvantagens de cada enfoque.
SCN
No SCN precisamos representar toda e qualquer operação de navegação ou zoom através de uma transformação matricial.
Vantagens: É uma solução simples e elegante. O seu programa gráfico vai ficar compacto, fácil de ler e entender e fácil de manter. Uma única rotina de transformação bastante simples em termos de código realiza tudo.
Desvantagens: Se você possui um mundo muito complexo e não possui um hardware acelerador gráfico onde implementar isso, o seu programa vai ficar lento, realizando sempre uma grande quantidade de cálculos matriciais a cada operação de navegação.
CPP
No CPP apenas operações de rotação exigem um recálculo da representação do mundo em CPP. As outras operações podem ser realizadas diretamente na representação existente através de somas ou operações de escala, sem necessidade de utilização de cálculo matricial.
Vantagens: É uma solução muito mais rápida e indicada se você vai implementar todo seu sistema gráfico em software e sem utilizar bibliotecas aceleradoras de algum hadware específico.
Desvantagens: Cria um conjunto de exceções, pois navegação linear é tratada de uma forma, zoom de outra e rotação de uma terceira. O seu código não vai ficar tão elegante e vai ficar mais difícil de manter.
O que é clipping?
Clipping ou recorte é um procedimento para a otimização do processo de cálculo da visualização dos objetos do display file, eliminando desse cálculo as primitivas geométricas que não se encontram sob a window e particionado as primitivas geométricas parcialmente aparentes. Opera no sistema de coordenadas utilizado pela window. Seus objetivos são:
- Distinguir se primitivas geométricas estão dentro ou fora do viewing frustum (regiões do espaço especificadas);
- Distinguir se primitivas geométricas estão dentro ou fora do picking frustum, regiões do espaço que podem interagir com o mouse;
- Detectar intersecções entre primitivas;
- Calcular sombras (em 3D)
Clipping é uma otimização importante por:
- Ser o preprocessamento de visibilidade;
- Remover uma fração considerável do mundo antes de se realizar o cálculo de visualização;
- Assegurar que somente primitivas potencialmente visíveis serão rasterizadas.
Conceitos Básicos
O conceito geométrico básico do recorte é a clip window:
- A região para a qual um objeto deve ser recortado;
- A forma geométrica de recorte;
- Normalmente corresponde à window;
Sempre realizamos recorte em coordenadas da clip window::
- Recorte de pontos (point clipping);
- Recorte de linhas (line clipping);
- Recorte de áreas e polígonos (area and polygon clipping);
- Recorte de curvas (curve clipping);
- Recorte de texto (text clipping);
Destes cinco, os dois mais utilizados e mais importantes são o recorte de pontos e o recorte de linhas. Utilizando apenas estes dois, você consegue realizar uma implementação bastante eficiente de um SGI, desde que os objetos neste SGI sejam representados apenas por linhas (modelos de arame). Se você utilizar áreas (2D) ou superfícies (3D) preenchidas, representadas por polígonos preenchidos ou hachurados, você vai precisar ainda do recorte de áreas e polígonos. O recorte de curvas torna um SGI que representa curvas mais eficiente, mas como toda curva no fim de contas é desenhada como um polígono, pode ser realizado através de recorte de linhas ou de polígonos, dependendo se for cheia ou não.
Recorte de Pontos
Para uma clip window retangular, o recorte de pontos ou point clipping é um processo rápido e muito simples. O ponto que deve ser apresentado na viewport é aquele para o qual as inequações abaixo são satisfeitas:
Recorte de Linhas
Existem vários relacionamentos possíveis com uma região de clipping retangular. Estes relacionamentos possíveis são:
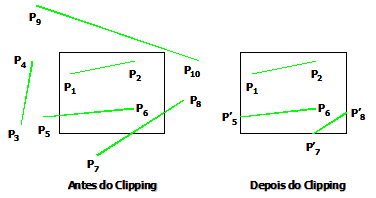 |
Recorte de Linhas usando representação paramétrica da reta
Este método utiliza a verificação por meio da equação paramétrica envolvendo os limites da janela e a própria linha:
- Grande quantidade de cálculos e teste e não é muito eficiente. Num display típico, centenas ou milhares de linhas de linha podem ser encontradas.
Recorte de Linhas de Cohen-Sutherland:
Este método utiliza uma representação das extremas dos segmentos de reta associada a códigos de regiões.
Estes códigos são códigos de região binários de 4 dígitos atribuídos a todo ponto final de uma linha na figura. São chamados region codes (RC).
Numera-se as posições no código de regiões de 1 a 4. Cantos são representados por soma de valores, como mostra a See Códigos binários de regiões para recorte.
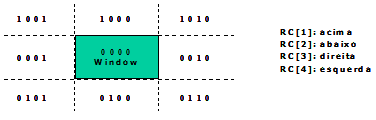 |
Os valores dos códigos de região são determinados através da comparação das coordenadas das extremidades aos limites da window. Um valor 1 em qualquer posição indica que o ponto está neste quadrante.

Existem três possíveis relacionamentos:
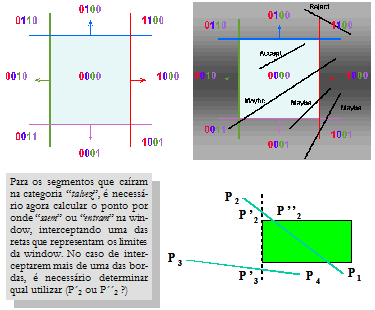 |

Exemplo de aplicação de recorte com Cohen-Sutherland
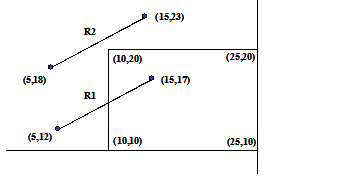 |
Entenderemos melhor o algoritmo acima através de um exemplo. Para isso observe as duas retas paralelas na figura abaixo. Vamos clipar passo a passo estas retas utilizando o algoritmo de Cohen Sutherland.
- RC1 = [0001] -> esquerda e RC2 = [0000] -> dentro
- Cálculo do coeficiente angular:
- Aplicamos a fórmula esq.: yintersec = m* (xE – x1) + y1
- Como 14.5 > yF = 10 e 14.5 < yT = 20 aceitamos.
RC1 = [0001] -> esquerda e RC2 = [1000] -> topo
- Clipamos à esquerda e calculamos novo y1 para a linha.
- Clipamos ao topo e calculamos novo x2 para a linha
Cálculo do coeficiente angular:
Aplica-se a fórmula esq.: yintersec = m* (xE – x1) + y1
Como 20.5 > yF = 10 mas 20.5 não é < yT = 20 rejeitamos.
- Intersecção é fora da window
- Não é necessário calcular x2 – se uma intersecção for fora a outra também o será.
O segmento de reta R2 é descartado como não visível.
O resultado obtido será o mostrado na figura abaixo.
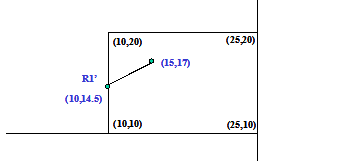 |
 |
Como procedemos quando um ponto cair em um dos cantos?
Observe o exemplo da See Conjunto de retas a serem recosrtas com Liang-Barsky. Quando o RC associado a um ponto de uma linha possuir dois “1”, calculamos a intersecção com as bordas da window para os dois casos.
Aceitamos dentre os dois valores calculados, aquele que se encontrar sobre a window
Recorte de linhas de Liang-Barsky
Em 1978 Cyrus e Beck publicaram um novo algoritmo para o clipping de linhas usável para clipar linhas contra um polígono convexo em 2D ou um poliedro convexo em 3D usando a equação paramétrica. Em 1984 Liang e Barsky reformularam este algoritmo, tornando-o mais eficiente. Esta versão será vista a seguir. Reescreva as equações paramétricas como segue:
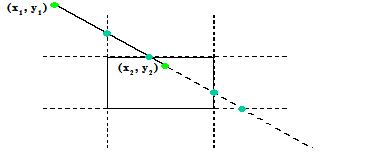 |
Os parâmetros u1 and u2 definem qual parte está dentro do retângulo:
Exemplo detalhado usando Liang-Barsky
Calculemos detalhadamente um exemplo usando Liang-Barsky. Para tanto tome a figura abaixo como ponto de partida.
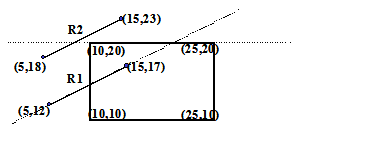 |
- p1 = -Dx = -(15 – 5) = -10
- p2 = Dx = 15 – 5 = 10
- p3 = -Dy = -(17 – 12) = -5
- p4 = Dy = 17 – 12 = 5
- q1 = x1 – xwmin= 5 – 10 = -5
- q2 = xwmax – x1 = 25 – 5 = 20
- q3 = y1 – ywmin= 12 – 10 = 2
- q4 = ywmax – y1 = 20 – 12 = 8

u1 = max (0, r1, r3) = max (0, 0.5, -0.4) = 0.5
Substituindo na equação paramétrica:
x = 5 + 0.5 * 10 = 10 (o que nós já sabíamos)
y = 12 + 0.5 * 5 = 14.5 (o que nós não sabíamos)
u2 = min (1, r1, r3) = min (1, 2, 1.6) = 1
Como u2 resulta 1, rejeitamos o cálculo de novos valores de dentro para fora.
Recorte de linhas de Nicholl-Lee-Nicholl
A algoritmo de Nicholl-Lee-Nicholl utiliza uma forma bastante diferente de determinação da intersecção entre o segmento de reta examinado e os limites da window.
Toma-se um ponto do segmento de reta, P1, e divide-se a imagem em quadrantes, traçando novos segmentos de reta passando pelos vértices da window. Depois verifica-se em qual dos quadrantes P2 se encontra, simplesmente comparando as inclinações da retas que criamos interligando P1 e os vértices da wundow e o segmento que queremos clipar. Quando determinamos qual o quadrante, calculamos a intesecção de retas apenas com o lado da window que está neste quadrante.
Comparado NLN aos algoritmos C-S e L-B:
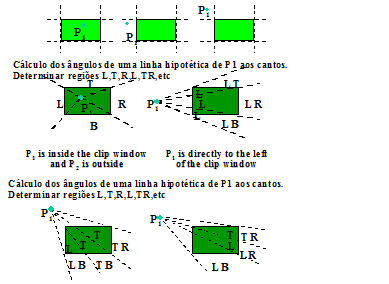 |
- Clipa uma linha com extremas P1 e P2;
- 1º passo: determinar P1 para os nove quadrantes:
- 2º passo: determinar a posição de P2 em relação a P1
Para determinar em qual região P2 está:
- Compare-se a inclinação da reta com as inclinações das retas hipotéticas calculadas. Ex: P1 está à esquerda, P2 está em LT.

Clip windows não retangulares
Em algumas situações especiais teremos windows não retangulares. Isto geralmente acontece quando a aplicação, por alguma razão estética, utiliza uma viewport não retangular. O sistema de janelas do sistema operacional NeXTSTEP, da linha de computadores NeXT, uma tentativa de um sócio da Apple de fazer algo diferente do Macintosh, utilizando um processador Motorola 68040, por exemplo, possuía planejada a possibilidade de se desenvolver aplicações com janelas redondas ou ovais.
 |
Para trabalhar com windows não convencionais, algumas técnicas foram desenvolvidas. Vamos apenas citá-las resumidamente aqui:
Recorte de windows na forma de polígonos côncavos:
Identificar se um polígono é côncavo:
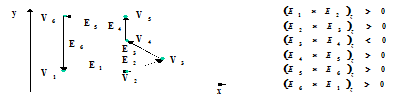 |
- Uma componente z negativa resultante da multiplicação posicionada entre componentes positivas indica uma concavidade local;
Divisão de polígonos côncavos: método vetorial
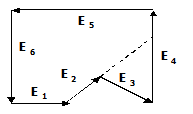 |
Outra opção é rotacionar o polígono sobre o eixo x aresta a aresta e verificar se há interesecção de alguma outra aresta com este eixo. Se houver, o intersecção já vai mostrar como subdividir o polígono em subpolígonos convexos.
 |
Após a rotacionar V3 em torno do eixo x, V4 está abaixo do eixo x.
O corte do poligono é realizado através da linha entre os pontos V2V3.
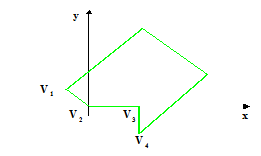
Recorte de polígonos
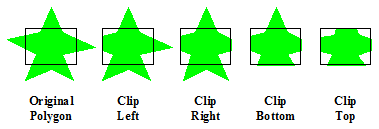
Recortar objetos de formato poligonal na cena pode ser tratado como recorte de linhas quando os polígonos são vazios. Quando os polígonos são preenchidos, este método já não traz mais resultados satisfatórios, como mosra a See Comparação entre clipping de polígonos como linhas clipping real de polígonos..
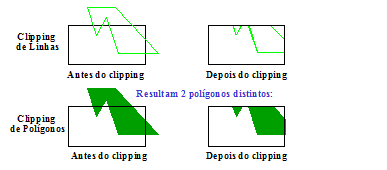 |
Recorte de polígonos de Sutherland-Hodgeman
Este método processa as bordas do polígono como um todo contra cada aresta do window:
 |
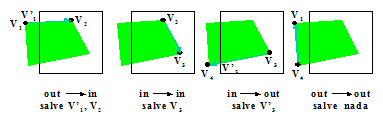 |
Recorte de polígonos de Weiler-Atherton
O algoritmo de Weiler-Atherton é o mais genérico algoritmo de recorte para polígonos e recorta um polígono côncavo com buracos interiores em relação aos limites de outro polígono côncavo, que também pode possuir buracos interiores. Na terminologia do algoritmo de Weiler-Atherton, o polígono a ser recortado é chamado de polígono-objeto e a região de recorte é chamada de polígono de recorte. As novas arestas do polígono-objeto, criada por seu recorte contra o poilígono de recorte, são idênticas a partes do polígono de recorte. O clipping de polígonos de Weiler-Atherton foi desenvolvido para identificação de superfícies visíveis.
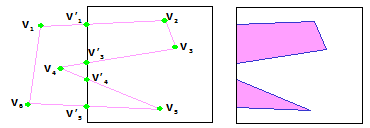 |
- Pode ser aplicado a uma região de recorte arbitrária;
- Pode ser usado para seguir as bordas de qualquer coisa com qualquer formato;
Se processamos em sentido horário procedemos assim:
- Para um par de vértices de fora para dentro, siga a aresta do polígono;
- Para um par de vértices de dentro para fora, siga o limite da window em sentido horário.
Detalhamento do método de Weiler-Atherton
A implementação do algoritmo de W-A utiliza uma lista circular de vértices para descrever o polígono de recorte e todos os polígonos-objeto. Escolhe-se como convenção percorrer o polígono de recorte e os polígonos-objeto externos de objetos com limite polígonal sempre no sentido horário e os limites internos de objetos com furos no sentido anti-forário. Desta forma a superfície ou área cheia do objeto delimitado pelo polígono está sempre à direita. As arestas do polígono de recorte e dos polígonos-objeto podem ou não intersectar. Caso o façam, isto ocorre sempre aos pares, uma de entrada e outra de saída.
O algoritmo inicia o processamento em alguma intersecção inicial e segue a borda externa do polígono-objeto em sentido horário até encontrar outra intersecção. Na interseção, dobra-se à direita e segue-se o exterior do polígono de recorte em sentido horário até encontrar uma intersecção com o polígono-objeto. Nesta intersecção dobra-se novamente à direita e segue-se o polígono-objeto. O processo é realizado até se voltar ao ponto de partida. Limites interiores do polígono-objeto são seguidos em sentido anti-horário.

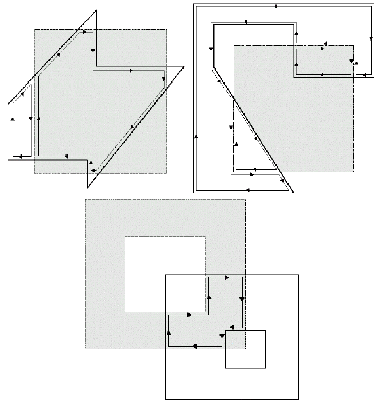 |
Outros tipos de Recorte
Além dos métodos de recorte vistos até agora, existem ainda alguns outros, específicos para aplicações avançadas ou para programas de desenho e design gráfico. Veremos resumidamente adiantes estes métodos.
Recorte de curvas
O recorte de curvas em SGIs utilizando modelos de arame, como veremos adiante, nos Capítulos 4 e 7, pode ser realizado através de métodos de recorte de linhas aplicados durante o processo de desenho das curvas 2D ou superfícies 3D. Se desejarmos uma representação eficiente e rápida de mundos contendo muitas curvas ou uma renderização realista em 3D de superfícies curvas preenchidas utilizando técnicas de renderização de raytracing como conversão por varredura, vistas no capítulo 8 e seguintes, teremos de possuir uma forma eficiente de realizar o recorte dessa curvas ou superfícies. Isto é especialmente importante em 3D, onde necessitamos determinar o polígono que representa a parte visível de uma superfície curva antes de iniciar o raytracing.
Existe um conjunto de técnicas bastante simples para recorte eficiente de curvas baseado na idéia de se usar o casco convexo da curva, que em curvas cúbicas é um losango, para testar se a curva se encontra totalmente dentro, totalmente fora ou parcialmente dentro da window. A partir daí pode-se utilizar diferentes graus de refinamento para determinar o ponto da curva que entra ou sai da window. Um algoritmo bastante utilizado para isso é denominado Bézier-Clipping justamente por se aproveitar da propriedade de casco convexo das curvas de Bézier e uma excelente análise dele, além de outras referências, se encontram em .
Para o recorte de círculos usa-se as coordenadas de quadrantes individuais, dividindo o círculo em quadrantes e verificando a pertinência destes à window. Recursivamente o algoritmo devide as partes parcialmente contidas na window. Neste processo recursivo pode-se primeiramente gerar octantes e depois ir diminuindo no segmento onde a pertinência for parcial.
O clipping de texto pode ser realizado de duas formas diferentes. Em ambas as formas utiliza-se um casco convexo, que é ou definido ao redor do texto todo ou ao redor de cada caractere:
- All-or-none string-clipping: Tomar limites do casco convexo de um string como todo e verificar a pertinência total deste polígono à window utilizando a regra de pertinência dos pontos extremos;
- All-or-none character-clipping: Tomar limites do casco convexo de carateres individuais pela regra de pertinência do ponto;
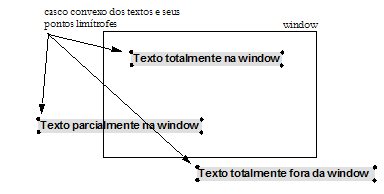 |
O método all-or-none string-clipping é o mais eficiente dos dois, mas possui a desvantagem de descartar strings parcialmente na window, como o texto mais à esquerda na See Recorte de texto pelo método all-or-none string-clipping.
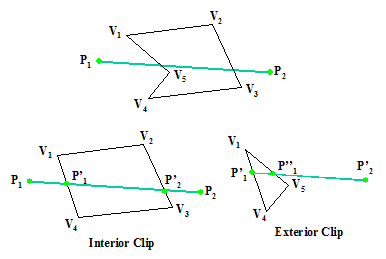 |
Recorte exterior
O clipping nem sempre é aplicado somente para determinar a pertinência de objetos ao interior de um polígono. Algumas vezes podemos desejar realizar o recorte exterior, isto é, determinar que partes de um objeto estão de fora de um polígono.
Isto serve para salvar uma região externa e possui aplicação em sistemas de windows múltiplos e em sistemas de desenho, durante a montagem de layouts de páginas para design em softwares como Corel Draw, Adobe Photoshop, Paint Shop, Gimp e outros.
Ao realizar o recorte externo, uilizamos os mesmos procedimentos de recorte utilizados para o interior de polígonos côncavos, apenas tomando os pontos “externos” à região de recorte como sendo os pontos remanescentes no processo.
Exercício 1.3: Implementando Clipping
Parte I: Implementando recorte para os objetos já existentes em seu SGI
Implemente uma as principais técnicas de clipagem para windows retangulares vistas neste capítulo, usando clipagem de pontos e clipagem por C-S, L-B ou NLN para retas, de forma a integrá-las ao seu sistema gráfico de maneira que a transformada de viewport seja aplicada apenas aos objetos resultantes do clipping.
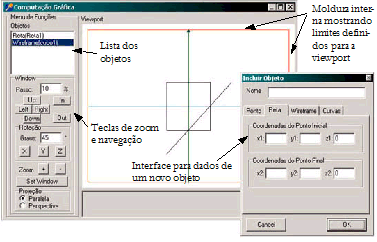 |
Para ter certeza de que a clipagem está funcionando e não é o algoritmo de clipagem de pontos embutido no seu objeto de interface que está fazendo com que as linhas que você está desenhando sejam cortadas no lugar certo, faça sua viewport ser menor do que o seu objeto de desenho (canvas, subcanvas ou outra coisa que você escolheu), de maneira que a viewport inicie em coordenadas do tipo 10,10 e termine antes do fim da área de desenho, cmo mostra a figura abaixo, onde a viewport está limitada pela moldura imediatamente interna à área de desenho. Dessa forma, se o seu algoritmo clipar algo de forma incorreta, deixando de recortar algum elemento, você vai enxergar imediatamente pois verá o objeto sair de dentro deste retângulo. Como forma de debugar seu exercíco este é um subterfúgio excelente e torna desnecessário analisar os dados gerados para uma lista enorme de objetos clipados para testar o sistema.
Parte II: Aumentando as capacidades de se SGI com cor e objetos preenchidos
Incremente agora o seu SGI estendendo a representação de seus objetos gráficos no display file para suportar cor e preenchimento. Para tanto crie dois novos atributos, cor e preenchimento na definição de sua classe de objeto2D.
O atributo cor deverá suportar a representação de cor utilizada pela linguagem de programação que você escolheu. Mais tarde, no Capítulo 11, vamos discutir a teoria da representação de cores em maiores detalhes. No momento você pode disponibiliar ao usuário um conjunto de cores básicas para ele escolher. A maioria das linguagens de programação define estas cores como constantes que podem ser utilizadas em programas.
O atributo preenchimento deverá ser uma variável booleana, que indica se um polígono fechado deve ser preenchido ou não. Observe que este atributo somente faz sentido para polígonos fechados e a lógica de seu programa deve levar isto em consideração, seja através da definição de uma hierarquia de diferentes classes de objetos 2D e da utilização de polimorfismo ou de outra técnica em linguagens de programação que não suportam polimorfismo. Não vamos discutir a modelagem de seu SGI aqui.
Com estes atributos deverá ser possível ao usuário definir objetos 2D poligonais preenchidos, que ao serem mostrados são desenhados como superfícies hachuradas ou preenchidas. Para implementar isto, utilize as funções de desenho de polígonos preenchidos fornecidas por sua linguagem de programação.
Para calcular a região visível de um polígono preenchido, que por sua vez é um novo polígono que deverá ser desenhado, implemente o algoritmo de Weiler-Atherton como algoritmo de recorte. Para simplificar a sua vida, considere apenas superfícies sem furos.