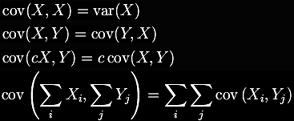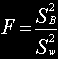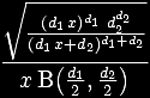Contents
- 1 5.5. Técnicas Estatísticas – Glossário de Termos Estatísticos
- 1.1 5.5.1. Variância
- 1.2 5.5.2. Desvio Padrão
- 1.3 5.5.3. Erro Padrão
- 1.4 5.5.4. Correlação
- 1.5 5.5.5. Autocorrelação
- 1.6 5.5.6. Covariância
- 1.7 5.5.7. Valor Esperado
- 1.8 5.5.8. Valor Estandardizado
- 1.9 5.5.9. Hipótese Nula
- 1.10 5.5.10. Análise de Variância – ANOVA
- 1.11 5.5.11. Teste F de Fisher
- 1.12 5.5.12. Distribuição-F de Fisher
5.5. Técnicas Estatísticas – Glossário de Termos Estatísticos
5.5.1. Variância
5.5.2. Desvio Padrão
5.5.3. Erro Padrão
5.5.4. Correlação
5.5.5. Autocorrelação
5.5.6. Covariância
5.5.7. Valor Esperado
5.5.8. Valor Estandardizado
5.5.9. Hipótese Nula
5.5.10. Análise de Variância – ANOVA
5.5.11. Teste F de Fisher
5.5.12. Distribuição-F de Fisher
5.5.1. Variância
A variância (este termo foi utilizado pela primeira vez por Fisher em 1918) de uma população de valores é calculada como:
s2 = S(xi–m)2/N
onde:
- m é a média da população
- N é o tamanho da população.
A estimativa amostral da variância de uma população finita de tamanho N é dada por: 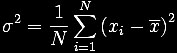
onde
- xbar é a média amostral
- N é o tamanho da amostra.
5.5.2. Desvio Padrão
In probability and statistics, the standard deviation is the most commonly used measure of statistical dispersion e a commonly-used measure of variation. O termo foi usado pela primeira vez por Pearson, 1894. Standard deviation is defined as the square root of the variância. It is defined this way in order to give us a measure of dispersion that is
- um número positivo e
- é expresso nas mesmas unidades dos dados.
Importante: We distinguish between the standard deviation s (sigma) of a whole population or of a random variable, and the standard deviation s of a sample.
O desvio padrão de uma população é calculado como:
s = [S(xi-m)2/N]1/2
onde:
- m is the population mean
- N is the population size
O desvio padrão de uma amostra é computado como:
s = [S(xi-xbar)2/n-1]1/2
onde:
- xbar is the sample mean
- n is the sample size.
5.5.3. Erro Padrão
The standard error of the mean (first used by Yule, 1897) is the theoretical standard deviation of all sample means of size n drawn from a population and depends on both the population variance (s) and the sample size (n) as indicated below:
sxbar = (s2/n)1/2onde:
- s2 is the population variance and
- n is the sample size.
5.5.4. Correlação
In probability theory and statistics, the correlation, also called coeficiente de correlação, between two random variables is found by dividing their covariância by the product of their standard deviations. (It is defined only if these standard deviations are finite.) It is a corollary of the Cauchy-Schwarz inequality that the correlation cannot exceed 1 in absolute value.
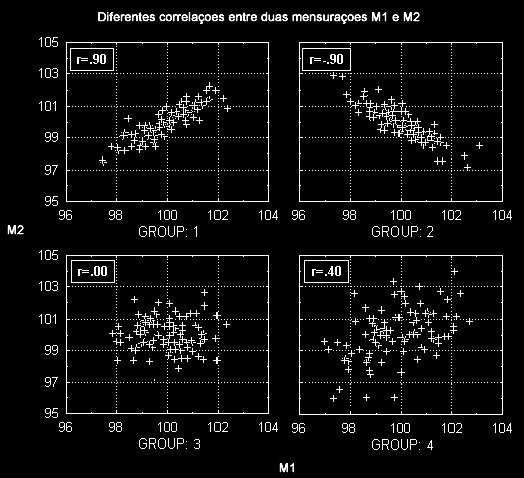
Redizendo isto em termos menos matemáticos, a correlation is a measure of the relation between two or more variables. Correlation coefficients can range from -1.00 to +1.00. The value of -1.00 represents a perfect negative correlation while a value of +1.00 represents a perfect positive correlation. A value of 0.00 represents a lack of correlation.
- Correlação Positiva. The relationship between two variables is such that as one variable’s values tend to increase, the other variable’s values also tend to increase. This is represented by a positive correlation coefficient.
- Correlação Negativa. The relationship between two variables is such that as one variable’s values tend to increase, the other variable’s values tend to decrease. This is represented by a negative correlation coefficient.
The most widely-used type of correlation coefficient is Pearson r (Pearson, 1896), also called linear or product-moment correlation (the term correlation was first used by Galton, 1888). It is the basic type of correlation. Using non technical language, one can say that the correlation coefficient determines the extent to which values of two variables are “proportional” to each other. The value of the correlation (i.e., correlation coefficient) does not depend on the specific measurement units used; for example, the correlation between height and weight will be identical regardless of whether inches and pounds, or centimeters and kilograms are used as measurement units. Proportional means linearly related; that is, the correlation is high if it can be approximated by a straight line (sloped upwards or downwards). This line is called the regression lineor least squares line, because it is determined such that the sum of the squared distances of all the data points from the line is the lowest possible.
Pearson correlation assumes that the two variables are measured on at least interval scales.
Significância de uma Correlação
The significance level calculated for each correlation is a primary source of information about the reliability of the correlation. The test of significance is based on the assumption that the distribution of the residual values (i.e., the deviations from the regression line) for the dependent variable y follows the normal distribution, and that the variability of the residual values is the same for all values of the independent variable x. However, Monte Carlo studies suggest that meeting those assumptions closely is not absolutely crucial if your sample size is not very large. It is impossible to formulate precise recommendations based on those Monte Carlo results, but many researchers follow a rule of thumb that if your sample size is 50 or more then serious biases are unlikely, and if your sample size is over 100 then you should not be concerned at all with the normality assumptions. There are, however, much more common and serious threats to the validity of information that a correlation coefficient can provide.
5.5.5. Autocorrelação
Autocorrelation is a mathematical tool used frequently in signal processing for analysing functions or series of values, such as time domain signals. Autocorrelation is useful for finding repeating patterns in a signal, such as determining the presence of a periodic signal which has been buried under noise, or identifying the fundamental frequency of a signal which doesn’t actually contain that frequency component, but implies it with many harmonic frequencies.
An autocorrelation is the cross-correlation of a signal with itself. It is the correlation of a series of data with itself, shifted by a particular lag of k observations. The plot of autocorrelations for various lags is a crucial tool for determining an appropriate model for ARIMA analysis. The computations of the autocorrelation coefficients rk follow the standard formulas, as described in most time series references (e.g., Box & Jenkins, 1976).
5.5.6. Covariância
A covariância duas variáveis randômicas X e Y, com expected values E(X) = m e E(Y) = n é definida como:
Isto é equivalente à fórmula abaixo, que é geralmente utilizada na realização dos cálculos:
For column-vector valued random variables X and Y with respective expected values ? and ?, and n and m scalar components respectively, the covariance is defined to be the n×m matrix
cov(X,Y) é também notada como CXY e denominada matriz de covariância.
If X and Y are independent, then their covariance is zero. This follows because under independence, E(X·Y) = E(X)·E(Y). The converse, however, is not true: it is possible that X and Y are not independent, yet their covariance is zero.
The covariance matrix is always symmetric and positive semi-definite. It is diagonal if all n variables are independent. Its determinant is zero if linear relations exist between variables.
If X and Y are real-valued random variables and c is a constant (“constant”, in this context, means non-random), then the following facts are a consequence of the definition of covariance:
For vector-valued random variables, cov(X, Y) and cov(Y, X) are each other’s transposes.
The covariance is sometimes called a measure of “linear dependence” between the two random variables. That phrase does not mean the same thing that it means in a more formal linear algebraic setting (see linear dependence), although that meaning is not unrelated.
The correlation is a closely related concept used to measure the degree of linear dependence between two variables.
5.5.7. Valor Esperado
The expectation value or mean of a random variable X or a function H(X) is given by:
for a discrete or continuous variable, respectively. The sum for discrete variables is extended over all possible values of xi, where P(X=xi) are the corresponding probabilities. For continuous variables, the probability density is f(x). The concept is readily generalized for several random variables by replacing X by ![]() .
.
The expectation value is a linear operator. The expectation value of a function is sometimes written Ex(H) instead of E(H(x)).
Traduzindo isto em termos menos abstratos, the expected value (or expectation) of a random variable is the sum of the probability of each possible outcome of the experiment multiplied by its payoff (“value”). Thus, it represents the average amount one “expects” to win per bet if bets with identical odds are repeated many times. Note that the value itself may not be expected in the general sense, it may be unlikely or even impossible.
For example, an American Roulette wheel has 38 equally possible outcomes. A bet placed on a single number pays 35-to-1 (this means that he is paid 35 times his bet, while also his bet is returned, together he gets 36 times his bet). So the expected value of the profit resulting from a $1 bet on a single number is, considering all 38 possible outcomes: ( -1 × 37/38 ) + ( 35 × 1/38 ), which is about -0.0526. Therefore one expects, on average, to lose over 5 cents for every dollar bet.
5.5.8. Valor Estandardizado
O valor estandardizado de uma distribuição de dados é também chamado de z-score ou valor transformado. Para a maioria dos métodos estatísticos se utiliza a estandardização dos dados. A estandardização é diferente da normalização dos dados, onde se objetiva que cada variável se encontre em uma faixa de valores no intervalo [0,1]. Na estandardização a faixa de valores pode variar e depende do desvio padrão e se utiliza a fórmula abaixo:
xestandardizado = (x – média)/desvio-padrão
calculada, como na normalização, de forma independente para cada variável. A estandardização toma informações sobre a média e o desvio padrão de uma variável e produz um valor correspondente a cada valor original que especifica a posição deste valor original dentro da distribuição original de dados.
O valor original, independentemente de pertencer a uma distribuição de dados que inclua valores negativos, é transformado em um valor com sinal, de tal forma que:
- O sinal indique se o valor original , também chamado de score, está acima (+) ou abaixo (-) da média.
- O módulo do valor estandardizado indique a distância entre entre a média e o valor original em termos de desvios-padrão .
Dessa forma, um valor estandardizado de -2,4 representa um valor original que se encontra mais de dois desvios-padrão abaixo da média, representando um valor bem defícil de ocorrer de de probabilidade muito baixa.
5.5.9. Hipótese Nula
Em estatística, a Hipótese Nula é a hipótese levantada com o objetivo de ser refutada com a finalidade de se aceitar uma Hipótese Alternativa. Quando utilizada, a hipótsese nula é presumida ser verdadeira até que evidência estatística na forma de um Teste de Hipótese indicar o contrário [wikipedia].
5.5.10. Análise de Variância – ANOVA
In statistics, analysis of variance (ANOVA) is a collection of statistical models and their associated procedures which compare means by splitting the overall observed variance into different parts. The initial techniques of the analysis of variance were pioneered by the statistician and geneticist R. A. Fisher in the 1920s and 1930s, and is sometimes known as Fisher’s ANOVA or Fisher’s analysis of variance, due to the use of Fisher’s F-distribution as part of the test of statistical significance.
Este verbete foi baseado em parte na [wikipedia].
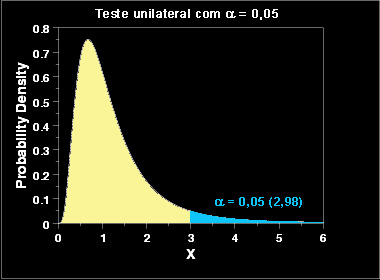
5.5.11. Teste F de Fisher
Um Teste-F é qualquer teste estatístico onde a estatística do teste possui uma distribuição-F se a hipótese nula for verdadeira. Uma grande variedade de hipóteses em Estatística Aplicada é testada através de testes-F. Os principais são:
- A hipótese de que as médias de múltiplas populações distribuídas normalmente, todas apresentando o mesmo desvio padrão, são iguais. Esta é provavelmente a mais conhecida hipótese testada través de um teste-F e é o problema básico na Análise de Variância (ANOVA).
- A hipótese de que os desvios padrão de duas populações são iguais e que conseqüentemente elas são de origem comparável.
Se é a igualdade de variâncias ou de desvios-padrão que está sendo testada, o teste-F é extremamente pouco robusto para distribuições diferentes da normalidade. Se os dados demonstram desvios da normalidade, mesmo que pequenos, desaconselha-se o uso do teste-F.
Entendendo o Significado do Valor de F calculado
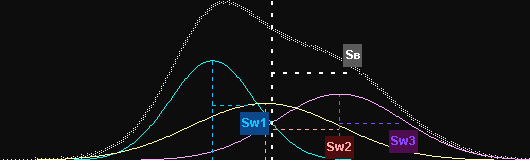
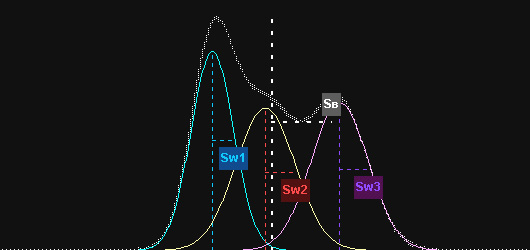
Na análise de variância o teste F oferece, diretamente, a decisão sobre a diferença entre as médias. Não há mistério: O teste que compara variâncias é o teste F. Considere, então, o caso da análise de variância, imaginando-se três amostras (Sw1, Sw2 e Sw3) representadas em turquesa, amarelo e lilás na figura abaixo:
Cada amostra tem sua média (linha vertical pontilhada) e medida de dispersão (Sw1, Sw2 e Sw3), dada pelo seu desvio-padrão. Podemos imaginar que, tomando-se as três amostras conjuntamente, exista uma média geral, com sua respectiva medida de dispersão (SB), dada pelo desvio-padrão global.
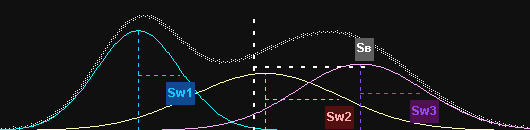
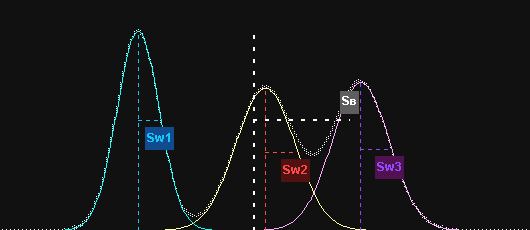
Caso a dispersão SW (dentro dos grupos) seja mantida, mas as médias de cada amostra sejam mais distantes entre si, aumenta-se a dispersão entre os grupos, SB como mostra a figura abaixo:
Como o teste F é dado por…
… onde SW2 é obtido por uma composição de Sw1, Sw2 e Sw3, se as médias são mais afastadas entre si, SB e F (conseqüentemente) aumentam.
Mantendo-se as mesmas médias da figura 1, mas diminuindo-se a dispersão entre os grupos (Sw#), o que sofre maior redução é o denominador, SW2, o que também leva a um aumento do valor de F (figura 3).
Compare, agora, esta última figura com as figuras 2 e 3 e verifique porque o valor F é diferente neste caso do que em todos os anteriores. Observe que, grosseiramente falando, quanto menos sobreposição entre as amostras, mais provavelmente o teste indicará significância estatística. As distribuições abaixo estão bastante separadas e muito provavelmente indicam situações diferentes de um mesmo fenômeno.
Usando o valor de F gerado
Até agora aprendemos a calcular F para um determinado caso específico. Temos agora de entender como testamos a nossa hipótese para aceitar ou rejeitar a hipótese nula.
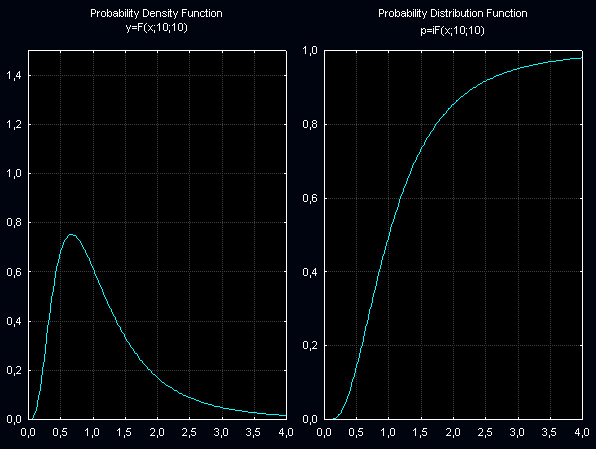
5.5.12. Distribuição-F de Fisher
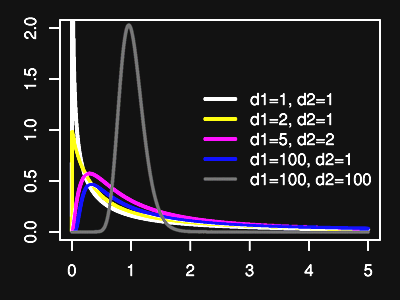
Função de Distribuição de Probabilidade-F para vários pares de graus de liberdade

Função de Distribuição de Probabilidade-F Acumulada para vários pares de graus de liberdade
Este verbete foi baseado em parte na [wikipedia].